题目内容
16.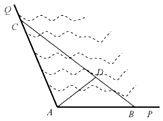 如图所示,∠PAQ是某海湾旅游区的一角,其中∠PAQ=120°,为了营造更加优美的旅游环境,旅游区管委员会决定在直线海岸AP和AQ上分别修建观光长廊AB和AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价为120万元,同时在线段BC上靠近点B的三等分点D处建一个观光平台,并建水上直线通道AD(平台大小忽略不计),水上通道的造价是1000元/米.
如图所示,∠PAQ是某海湾旅游区的一角,其中∠PAQ=120°,为了营造更加优美的旅游环境,旅游区管委员会决定在直线海岸AP和AQ上分别修建观光长廊AB和AC,其中AB是宽长廊,造价是800元/米;AC是窄长廊,造价是400元/米;两段长廊的总造价为120万元,同时在线段BC上靠近点B的三等分点D处建一个观光平台,并建水上直线通道AD(平台大小忽略不计),水上通道的造价是1000元/米.(1)若规划在三角形ABC区域内开发水上游乐项目,要求△ABC的面积最大,那么AB和AC的长度分别为多少米?
(2)在(1)的条件下,建直线通道AD还需要多少钱?
分析 (1)设AB=xm,AC=ym,则800x+400y=1200000,即2x+y=3000,表示面积,利用基本不等式,可得结论;
(2)利用向量方法,求出AD,即可得出结论.
解答 解:(1)设AB=xm,AC=ym,则800x+400y=1200000,即2x+y=3000,
S△ABC=$\frac{1}{2}xysin120°$=$\frac{\sqrt{3}}{4}xy$=$\frac{\sqrt{3}}{8}•2x•y≤\frac{\sqrt{3}}{8}•(\frac{2x+y}{2})^{2}$=281250$\sqrt{3}$m3,
当且仅当2x=y,即x=750m,y=1500m时等号成立,
∴△ABC的面积最大,那么AB和AC的长度分别为750米和1500米;
(2)在(1)的条件下,$\overline{AD}$=$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}\overrightarrow{AC}$,
∴${\overrightarrow{AD}}^{2}$=$\frac{4}{9}{\overrightarrow{AB}}^{2}+\frac{4}{9}\overrightarrow{AB}•\overrightarrow{AC}+\frac{1}{9}{\overrightarrow{AC}}^{2}$=250000,
∴|$\overrightarrow{AD}$|=500,
∴1000×500=500000元,即建直线通道AD还需要50万元.
点评 本题考查三角形中面积的求法,考查向量知识的运用,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
11.将函数y=sin(x-$\frac{π}{12}$)图象上的点P($\frac{π}{4}$,t)向左平移s(s>0)个单位,得到点P′,若P′位于函数y=sin2x的图象上,则( )
| A. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{6}$ | B. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{6}$ | ||
| C. | t=$\frac{1}{2}$,s的最小值为$\frac{π}{12}$ | D. | t=$\frac{\sqrt{3}}{2}$,s的最小值为$\frac{π}{12}$ |
1.已知函数y=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示,则φ=( )
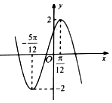

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
5.平面直角坐标系中,在直线x=1,y=1与坐标轴围成的正方形内任取一点,则此点落在曲线y=x2下方区域的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{9}$ | D. | $\frac{5}{9}$ |
6.从区间[0,1]随机选取三个数x,y,z,若满足x2+y2+z2>1,则记参数t=1,否则t=0,在进行1000次重复试验后,累计所有参数的和为477,由此估算圆周率π的值应为( )
| A. | 3.084 | B. | 3.138 | C. | 3.142 | D. | 3.136 |
