题目内容
13.已知向量$\overrightarrow{a}$=(x,2),$\overrightarrow{b}$=(2,x),若$\overrightarrow{a}$+2$\overrightarrow{b}$与2$\overrightarrow{a}$+$\overrightarrow{b}$夹角为$\frac{π}{2}$,则|$\overrightarrow{a}$-$\overrightarrow{b}$|=6$\sqrt{2}$或3$\sqrt{2}$.分析 根据向量垂直的等价条件求出x,结合向量的模长公式进行求解即可.
解答 解:∵$\overrightarrow{a}$+2$\overrightarrow{b}$与2$\overrightarrow{a}$+$\overrightarrow{b}$夹角为$\frac{π}{2}$,
∴($\overrightarrow{a}$+2$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=0,
∵$\overrightarrow{a}$=(x,2),$\overrightarrow{b}$=(2,x),
∴$\overrightarrow{a}$+2$\overrightarrow{b}$=(x+4,2+2x),2$\overrightarrow{a}$+$\overrightarrow{b}$=(2x+2,x+4),
则(x+4)(2+2x)+(2x+2)(x+4)=0,
即2(x+4)(2+2x)=0,
则x=-4或x=-1,
若x=-4,则$\overrightarrow{a}$=(-4,2),$\overrightarrow{b}$=(2,-4),$\overrightarrow{a}$-$\overrightarrow{b}$=(-6,6),|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{6}^{2}+{6}^{2}}$=6$\sqrt{2}$,
若x=-1,则$\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(2,-1),$\overrightarrow{a}$-$\overrightarrow{b}$=(-3,3),|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$,
故答案为:6$\sqrt{2}$或3$\sqrt{2}$,
点评 本题主要考查平面向量的应用,根据向量的垂直关系求出x的值,结合向量的模长公式进行计算是解决本题的关键.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案| A. | 8 | B. | 8+2△x | C. | 2(△x)2+8△x | D. | 4△x+2(△x)2 |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
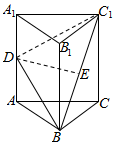 如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.