题目内容
8.计算下列各值:(不用计算器,写出必要的过程)(1)sin(arcsin$\frac{1}{2}$+arcsin$\frac{\sqrt{3}}{2}$);
(2)sin[arcsin$\frac{12}{13}$-arcsin(-$\frac{3}{5}$)];
(3)sin(π-2arcsin$\frac{4}{5}$)
分析 由条件利用反正弦函数的定义,两角和差的三角公式,求得所给式子的值.
解答 解:(1)∵arcsin$\frac{1}{2}$=$\frac{π}{6}$,arcsin$\frac{\sqrt{3}}{2}$=$\frac{π}{3}$,
∴sin(arcsin$\frac{1}{2}$+arcsin$\frac{\sqrt{3}}{2}$)=sin($\frac{π}{6}$+$\frac{π}{3}$)=sin$\frac{π}{2}$=1.
(2)sin[arcsin$\frac{12}{13}$-arcsin(-$\frac{3}{5}$)]
=sin(arcsin$\frac{12}{13}$)cos[arcsin(-$\frac{3}{5}$)]-cos(arcsin$\frac{12}{13}$)sin[arcsin(-$\frac{3}{5}$)]
=$\frac{12}{13}$•$\frac{4}{5}$-$\frac{5}{13}$•(-$\frac{3}{5}$)=$\frac{63}{65}$.
(3)sin(π-2arcsin$\frac{4}{5}$)=sin (2arcsin$\frac{4}{5}$)=2sin(arcsin$\frac{4}{5}$)cos(arcsin$\frac{4}{5}$)
=2•$\frac{4}{5}$•$\frac{3}{5}$=$\frac{24}{25}$.
点评 本题主要考查反正弦函数的定义,两角和差的三角公式的应用,属于基础题.

练习册系列答案
相关题目
16.过直线x-y-3=0与2x-y-5=0的交点,且与向量$\overrightarrow{n}$=(1,-3)垂直的直线方程是( )
| A. | x-3y-5=0 | B. | 3x+y-5=0 | C. | x+3y-5=0 | D. | x-y-5=0 |
3.函数f(x)=sin4x+acos4x图象的一条对称轴方程是直线x=$\frac{π}{6}$,则a=( )
| A. | 1 | B. | $\frac{\sqrt{3}}{3}$ | C. | -$\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
20.已知cos(α-$\frac{π}{3}$)=$\frac{1}{3}$,则sin(2α-$\frac{π}{6}$)的值为( )
| A. | -$\frac{4}{9}$$\sqrt{2}$ | B. | $\frac{4}{9}$$\sqrt{2}$ | C. | ±$\frac{4}{9}$$\sqrt{2}$ | D. | -$\frac{7}{9}$ |
17.在平面直角坐标系中,|$\overrightarrow{a}$|=2014,$\overrightarrow{a}$与x轴非负半轴的夹角为$\frac{π}{3}$,$\overrightarrow{a}$始点与原点重合,终点在第一象限,则向量$\overrightarrow{a}$的坐标是( )
| A. | (1007$\sqrt{2}$,1007$\sqrt{2}$) | B. | (-1007$\sqrt{2}$,1007$\sqrt{2}$) | C. | (1007,1007$\sqrt{3}$) | D. | (1007$\sqrt{3}$,1007) |
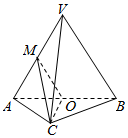 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O,M分别为AB,VA的中点.