Question

A是直二面角α-l-β的棱l上的一点，两条长为a的线段AB、AC分别在α、β内，且分别与l成45°角，则BC的长为（　　）

• A、a
• B、a或

  2

  a
• C、

  2

  a
• D、a或

  10

  2

  a

Answer 1

考点：点、线、面间的距离计算,二面角的平面角及求法

专题：空间位置关系与距离

分析：在一个直二面角内，由棱l上取一点A，过 A分别在 α、β 两个平面内作与棱成 45°的斜线AC、AB有两种作法，即当AC与AB同向和异向两种情况，在两条斜线上分别取点C和点B，借助于二面角是直二面角，构造直角三角形找边的关系，把要求解的角也放在一个三角形中，然后利用解三角形求解CD的大小．

解答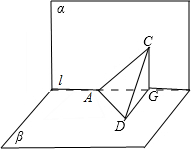： 解：如图，
当两斜线AC，AB同向时，在AC上取点C，过C作CG⊥l于G，
在平面β内过G作GB⊥l，交AB于B，连结CD．
∵二面角α-AB-β为直二面角，∴CG⊥β，则CG⊥GD．
在Rt△CGP中，∵∠CAG=45°，AB=AC=a，则AG=CG=

2

2

a．
在Rt△DGP中，∵∠BAG=45°，∴AB=AC=a，则DG=

2

2

a．
在Rt△DGC中，∵CG=DG=

2

2

a，∴CD=a．
如图：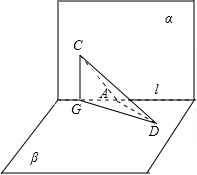
当两斜线AC，AB异向时，在AC上取点C，过C作CG⊥l于G，
在AB上取点B，使AB=AC=a，连结CD，
∵二面角α-AB-β为直二面角，∴CG⊥β，则CG⊥GD．
在Rt△CGA中，∵∠CAG=45°，∴AG=CG=

2

2

a，
AB=a，AG=

2

2

a，∠BAG=135°．
在△DPG中，GD²=AG²+AB²-2AG•ABcos135°
=a²+

1

2

a²-2•a•

2

2

a•（-

2

2

）=2a²．
∴CD²=CG²+GD²=

1

2

a²+2a²=

5

2

a²．
CD=

10

2

a
故选：D．

点评：本题考查了空间两条直线所成的角，考查了学生的空间想象能力和思维能力，考查了分类讨论的数学思想方法，是中档题．