题目内容
已知函数f（x）=x3-3x2+5 求该函数的单调区间和极值，求函数在区间[-1，3]上的最值．
考点：利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究函数的极值
专题：导数的综合应用
分析：求导数f′（x），解不等式f′（x）＞0，f′（x）＜0，即可得单调区间，由极值定义可求得极值；求出函数在区间端点处的函数值，与极值作比较，其中最大者为最大值，最小者为最小值；
解答：
解：函数f（x）=x3-3x2+5，所以f′（x）=3x2-6x，
由f′（x）＞0，即3x2-6x＞0，得x＜0或x＞2，由f′（x）＜0，得0＜x＜2，
所以f（x）的增区间是（-∞，0），（2，+∞），减区间是（0，2）．
所以当x=0时f（x）取得极大值f（0）=5，当x=2时f（x）取得极小值f（2）=1．
函数在区间[-1，3]时，f（-1）=1，f（3）=5，又由（0）知极大值f（0）=5，极小值f（2）=1，
所以f（x）在[-1，3]上的最大值为5，最小值为1．
由f′（x）＞0，即3x2-6x＞0，得x＜0或x＞2，由f′（x）＜0，得0＜x＜2，
所以f（x）的增区间是（-∞，0），（2，+∞），减区间是（0，2）．
所以当x=0时f（x）取得极大值f（0）=5，当x=2时f（x）取得极小值f（2）=1．
函数在区间[-1，3]时，f（-1）=1，f（3）=5，又由（0）知极大值f（0）=5，极小值f（2）=1，
所以f（x）在[-1，3]上的最大值为5，最小值为1．
点评：本题考查利用导数研究函数的单调性、极值与闭区间上的最值问题，准确求导，弄清导数与函数性质间的关系是解题关键．
练习册系列答案
阅读快车系列答案
相关题目
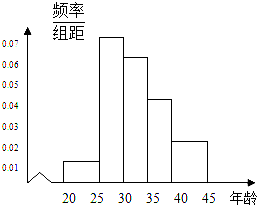南昌市为增强市民的交通安全意识，面向全市征召“小红帽”志愿者在部分交通路口协助交警维持交通，把符合条件的1000名志愿者按年龄分组：第1组[20，25）、第2组[25，30）、第3组[30，35）、第4组[35，40）、第5组[40，45），得到的频率分布直方图如图所示：