题目内容
在△ABC中,已知(sinA+sinB+sinC)(sinB+sinC-sinA)=3sinBsinC.
(1)求角A的大小;
(2)设O为△ABC的外心(三角形各边中垂线的交点),当BC=
,△ABC的面积为3
时,求
•
的值;
(3)设AD为△ABC的中线,当BC=2
时,求AD长的最大值.
(1)求角A的大小;
(2)设O为△ABC的外心(三角形各边中垂线的交点),当BC=
| 13 |
| 3 |
| AO |
| BC |
(3)设AD为△ABC的中线,当BC=2
| 3 |
考点:三角函数中的恒等变换应用,平面向量数量积的运算
专题:计算题,三角函数的求值,解三角形,平面向量及应用
分析:(1)由正弦定理将角化为边,再由余弦定理,即可求得A;
(2)运用余弦定理和面积公式,计算可得b,c,再由向量的数量积的定义和等腰三角形的性质,即可计算得到;
(3)由余弦定理,结合基本不等式可得b2+c2≤24,再由余弦定理求得中线长与b,c的关系,即可得到AD的最大值.
(2)运用余弦定理和面积公式,计算可得b,c,再由向量的数量积的定义和等腰三角形的性质,即可计算得到;
(3)由余弦定理,结合基本不等式可得b2+c2≤24,再由余弦定理求得中线长与b,c的关系,即可得到AD的最大值.
解答:
 解:(1)由(sinA+sinB+sinC)(sinB+sinC-sinA)=3sinBsinC,
解:(1)由(sinA+sinB+sinC)(sinB+sinC-sinA)=3sinBsinC,
运用正弦定理可得,(a+b+c)(b+c-a)=3bc,
即(b+c)2-a2=3bc,即b2+c2-a2=bc,
由余弦定理可得cosA=
=
=
,
由A为三角形的内角,则A=60°;
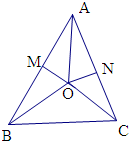
(2)如图O为△ABC的外心,连接OB,OC.
取AB的中点M,AC的中点为N,连接OM,ON,
则OM⊥AB,ON⊥AC,
由余弦定理得a2=b2+c2-2bccos60°,
即13=b2+c2-bc,
又S=
bcsin60°=
bc=3
,
即有bc=12,
解得b=3,c=4或b=4,c=3.
则
•
=
•(
-
)=
•
-
•
=|
|•|
|-|
|•|
|=
b2-
c2=
×(32-42)=-
或=
×(42-32)=
;
(3)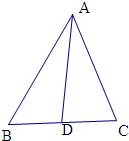 由余弦定理可得a2=b2+c2-2bccos60°,
由余弦定理可得a2=b2+c2-2bccos60°,
即12=b2+c2-bc,
由2bc≤b2+c2,
可得12≥
(b2+c2),
即b2+c2≤24,当且仅当b=c取等号.
由余弦定理可得cos∠ADB=
,cos∠ADC=
,
∠ADB+∠ADC=π,可得cos∠ADB+cos∠ADC=0,
即有6+2AD2=b2+c2,
则有6+2AD2≤24,解得AD≤3.
当且仅当b=c=2
时,AD取最大值3.
 解:(1)由(sinA+sinB+sinC)(sinB+sinC-sinA)=3sinBsinC,
解:(1)由(sinA+sinB+sinC)(sinB+sinC-sinA)=3sinBsinC,运用正弦定理可得,(a+b+c)(b+c-a)=3bc,
即(b+c)2-a2=3bc,即b2+c2-a2=bc,
由余弦定理可得cosA=
| b2+c2-a2 |
| 2bc |
| bc |
| 2bc |
| 1 |
| 2 |
由A为三角形的内角,则A=60°;
(2)如图O为△ABC的外心,连接OB,OC.
取AB的中点M,AC的中点为N,连接OM,ON,
则OM⊥AB,ON⊥AC,
由余弦定理得a2=b2+c2-2bccos60°,
即13=b2+c2-bc,
又S=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
即有bc=12,
解得b=3,c=4或b=4,c=3.
则
| AO |
| BC |
| AO |
| AC |
| AB |
| AO |
| AC |
| AO |
| AB |
=|
| AM |
| AC |
| AN |
| AB |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 2 |
或=
| 1 |
| 2 |
| 7 |
| 2 |
(3)
 由余弦定理可得a2=b2+c2-2bccos60°,
由余弦定理可得a2=b2+c2-2bccos60°,即12=b2+c2-bc,
由2bc≤b2+c2,
可得12≥
| 1 |
| 2 |
即b2+c2≤24,当且仅当b=c取等号.
由余弦定理可得cos∠ADB=
| 3+AD2-c2 | ||
2
|
| 3+AD2-b2 | ||
2
|
∠ADB+∠ADC=π,可得cos∠ADB+cos∠ADC=0,
即有6+2AD2=b2+c2,
则有6+2AD2≤24,解得AD≤3.
当且仅当b=c=2
| 3 |
点评:本题考查正弦定理、余弦定理和面积公式的运用,同时考查向量的数量积的定义和基本不等式的运用,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
已知某几何体的三视图如图所示,则该几何体的体积是( )


A、8
| ||||
B、
| ||||
C、
| ||||
D、16
|
 如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D点作⊙O的切线交AC于E.若CE=1,CA=5,则BD=
如图,已知在△ABC中,AB=AC,以AB为直径的⊙O交BC于D,过D点作⊙O的切线交AC于E.若CE=1,CA=5,则BD=