题目内容
直线L经过点P(1,2),且被两直线L1:3x-y+2=0和 L2:x-2y+1=0截得的线段AB中点恰好是点P,求直线L的方程.
考点:直线的点斜式方程
专题:直线与圆
分析:设A(a,b),则B(2-a,4-b),由A、B分别在L1、L2上,解得:a=
,b=
,由此能求出直线L的方程.
| 1 |
| 5 |
| 13 |
| 5 |
解答:
解:设A(a,b),
∵P(1,2)是AB中点,∴B(2-a,4-b),
又∵A、B分别在L1、L2上,
∴方程组
,
解得:a=
,b=
,
∴kAP=-
,直线L方程为y-2=-
(x-1)
整理,得3x+4y-11=0.
∵P(1,2)是AB中点,∴B(2-a,4-b),
又∵A、B分别在L1、L2上,
∴方程组
|
解得:a=
| 1 |
| 5 |
| 13 |
| 5 |
∴kAP=-
| 3 |
| 4 |
| 3 |
| 4 |
整理,得3x+4y-11=0.
点评:本题考查直线方程的求法,是基础题,解题时要认真审题,注意中点坐标公式的合理运用.

练习册系列答案
相关题目
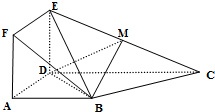 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD丄CD,AB∥CD,AB=AD=
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD丄CD,AB∥CD,AB=AD=