题目内容
对于定义域为[0,1]的函数f(x),如果同时满足以下三个条件:
①对任意的x∈[0,1],总有f(x)≥0
②f(1)=1
③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2)成立;则称函数f(x)为理想函数.
下面有三个命题:
①若函数f(x)为理想函数,则f(0)=0;
②函数f(x)=2x-1(x∈[0,1])是理想函数;
③若函数f(x)是理想函数,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f[f(x0)]=x0,则f(x0)=x0;
其中正确的命题个数有( )
①对任意的x∈[0,1],总有f(x)≥0
②f(1)=1
③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f(x1)+f(x2)成立;则称函数f(x)为理想函数.
下面有三个命题:
①若函数f(x)为理想函数,则f(0)=0;
②函数f(x)=2x-1(x∈[0,1])是理想函数;
③若函数f(x)是理想函数,假定存在x0∈[0,1],使得f(x0)∈[0,1],且f[f(x0)]=x0,则f(x0)=x0;
其中正确的命题个数有( )
| A、0个 | B、1个 | C、2个 | D、3个 |
考点:命题的真假判断与应用
专题:新定义
分析:(1)由①知:f(0)≥0;由③知f(0)≤0,从而得到f(0)=0.
(2)由题设知g(1)=1;由x∈[0,1]知2x∈[1,2],得g(x)∈[0,1],有g(x)≥0;设x1≥0,x2≥0,x1+x2≤1,则2x1≥1,2x2≥1;由此能够证明函数g(x)=2x-1在区间[0,1]上同时适合①②③.
(3)若f(x0)>x0,则由题设知f(x0)-x0∈[0,1],且由①知f[f(x0)-x0]≥0,由此入手能证明f(x0)=x0.
(2)由题设知g(1)=1;由x∈[0,1]知2x∈[1,2],得g(x)∈[0,1],有g(x)≥0;设x1≥0,x2≥0,x1+x2≤1,则2x1≥1,2x2≥1;由此能够证明函数g(x)=2x-1在区间[0,1]上同时适合①②③.
(3)若f(x0)>x0,则由题设知f(x0)-x0∈[0,1],且由①知f[f(x0)-x0]≥0,由此入手能证明f(x0)=x0.
解答:
解解:(1)由①知:f(0)≥0;由③知:f(0+0)≥f(0)+f(0),即f(0)≤0;
∴f(0)=0,①正确,
(2 ) 由题设知:g(1)=2-1=1;
由x∈[0,1]知2x∈[1,2],得g(x)∈[0,1],有g(x)≥0;
设x1≥0,x2≥0,x1+x2≤1,则2x1≥1,2x2≥1;
∴g(x1+x2)-[g(x1)+g(x2)]=(2x1+x2-1)-[(2x1-1)+(2x2-1)]=(2x1-1)(2x2-1)≥0
即g(x1+x2)≥g(x1)+g(x2)
∴函数g(x)=2x-1在区间[0,1]上同时适合①②③.②正确,
(3)证明:若f(x0)>x0,则由题设知:f(x0)-x0∈[0,1],且由①知f[f(x0)-x0]≥0,
∴由题设及③知:x0=f(f(x0))=f[(f(x0)-x0)+x0]≥f[f(x0)-x0]+f(x0)≥f(x0)矛盾;
若f(x0)<x0,则由题设知:x0-f(x0)∈[0,1],且由①知f[x0-f(x0)]≥0,
∴同理得:f(x0)=f[(x0-f(x0))+f(x0)]=f[x0-f(x0)]+f(f(x0))≥f(f(x0))=x0,矛盾;
故由上述知:f(x0)=x0.③正确.
故选:D.
∴f(0)=0,①正确,
(2 ) 由题设知:g(1)=2-1=1;
由x∈[0,1]知2x∈[1,2],得g(x)∈[0,1],有g(x)≥0;
设x1≥0,x2≥0,x1+x2≤1,则2x1≥1,2x2≥1;
∴g(x1+x2)-[g(x1)+g(x2)]=(2x1+x2-1)-[(2x1-1)+(2x2-1)]=(2x1-1)(2x2-1)≥0
即g(x1+x2)≥g(x1)+g(x2)
∴函数g(x)=2x-1在区间[0,1]上同时适合①②③.②正确,
(3)证明:若f(x0)>x0,则由题设知:f(x0)-x0∈[0,1],且由①知f[f(x0)-x0]≥0,
∴由题设及③知:x0=f(f(x0))=f[(f(x0)-x0)+x0]≥f[f(x0)-x0]+f(x0)≥f(x0)矛盾;
若f(x0)<x0,则由题设知:x0-f(x0)∈[0,1],且由①知f[x0-f(x0)]≥0,
∴同理得:f(x0)=f[(x0-f(x0))+f(x0)]=f[x0-f(x0)]+f(f(x0))≥f(f(x0))=x0,矛盾;
故由上述知:f(x0)=x0.③正确.
故选:D.
点评:本题考查函数值的求法和函数恒成立问题的应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
设集合U={0,1,2,3,4,5},M={0,3,5},N={1,4,5},则M∩(∁UN)=( )
| A、{5} |
| B、{0,3} |
| C、{0,2,3,5} |
| D、{0,1,3,4,5} |
关于A到B的一一映射,下列叙述正确的是( )
①一一映射又叫一一对应
②A中的不同元素的像不同
③B中每个元素都有原像
④像的集合就是集合B.
①一一映射又叫一一对应
②A中的不同元素的像不同
③B中每个元素都有原像
④像的集合就是集合B.
| A、①② | B、①②③ |
| C、②③④ | D、①②③④ |
在△ABC中,a,b,c分别为角A、B、C的对边,a=4,b=4
,∠A=30°,则∠B等于( )
| 3 |
| A、30° |
| B、30°或150° |
| C、60° |
| D、60°或120° |
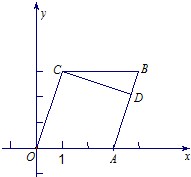 如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.
如图,在平行四边形OABC中,点A(3,0),C(1,3),过点C做CD⊥AB于点D.