题目内容
7.某自助银行有A,B,C三台ATM机,在某一时刻这三台ATM机被占用的概率分别为$\frac{1}{2}$,$\frac{1}{3}$,$\frac{2}{5}$,且这三台ATM机是否被占用互不影响.(1)如果某客户只能使用A或B这两台ATM机,求该客户不需要等待的概率;
(2)若X表示在该时刻这三台ATM机被占用的数量,求随机变量X的分布和数学期望.
分析 (1)先计算客户需要等待的概率,进而根据对立事件概率减法公式,得到答案;
(2)X的可能取值为0,1,2,3,进而可求出随机变量X的分布和数学期望.
解答 解:(1)设“该客户不需要等待”为事件M,
∵在某一时刻A,B两台ATM机被占用的概率分别为$\frac{1}{2}$,$\frac{1}{3}$,
P(M)=1-$\frac{1}{2}$×$\frac{1}{3}$=$\frac{5}{6}$,
∴客户不需要等待的概率为 $\frac{5}{6}$;
(2)由题意可得X的可能取值为0,1,2,3,
由(1)知P(X=0)=(1-$\frac{1}{2}$)(1-$\frac{1}{3}$)(1-$\frac{2}{5}$)=$\frac{1}{5}$,
P(X=1)=$\frac{1}{2}$(1-$\frac{1}{3}$)(1-$\frac{2}{5}$)+(1-$\frac{1}{2}$)$\frac{1}{3}$(1-$\frac{2}{5}$)+(1-$\frac{1}{2}$)(1-$\frac{1}{3}$)$\frac{2}{5}$=$\frac{13}{30}$,
P(X=2)=$\frac{1}{2}$•$\frac{1}{3}$(1-$\frac{2}{5}$)+(1-$\frac{1}{2}$)$\frac{1}{3}$•$\frac{2}{5}$+$\frac{1}{2}$•(1-$\frac{1}{3}$)$\frac{2}{5}$=$\frac{3}{10}$,
P(X=3)=$\frac{1}{2}$•$\frac{1}{3}$•$\frac{2}{5}$=$\frac{1}{15}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{5}$ | $\frac{13}{30}$ | $\frac{3}{10}$ | $\frac{1}{15}$ |
点评 本题考查的知识点是对立事件概率减法公式,相互独立事件概率乘法公式,随机变量的分布列与期望,难度中档.

| A. | (1,2) | B. | (2,+∞) | C. | (-2,1) | D. | (-2,+∞) |
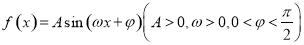 的图象经过三点
的图象经过三点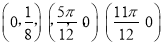 ,且在区间
,且在区间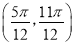 内有唯一的最值,且为最小值.
内有唯一的最值,且为最小值.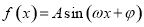 的解析式;
的解析式;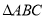 中,
中,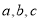 分别是角
分别是角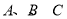 的对边,若
的对边,若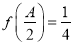 且
且 ,求
,求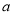 的值.
的值.