题目内容
4.两人掷一枚硬币,掷出正面多者为胜,但这枚硬币质地不均匀,以致出现正面的概率P1与出现反面的概率P2不相等,已知出现正面与出现反面是对立事件,设两人各掷一次成平局的概率为P,则P与0.5的大小关系是( )| A. | P<0.5 | B. | P=0.5 | C. | P>0.5 | D. | 不确定 |
分析 由已知得p=${{p}_{1}}^{2}+{{p}_{2}}^{2}$=${{p}_{1}}^{2}$+(1-p1)2=$2{{p}_{1}}^{2}-2{p}_{1}+1$,由此利用作差法能比较P与0.5的大小关系.
解答 解:∵这枚硬币质地不均匀,以致出现正面的概率P1与出现反面的概率P2不相等,
出现正面与出现反面是对立事件,设两人各掷一次成平局的概率为P,
∴p=${{p}_{1}}^{2}+{{p}_{2}}^{2}$=${{p}_{1}}^{2}$+(1-p1)2=$2{{p}_{1}}^{2}-2{p}_{1}+1$,
∵0≤p1≤1,且${p}_{1}=\frac{1}{2}$,
∴p-0.5=$2{{p}_{1}}^{2}-2{p}_{1}+1$-0.5=2(p1-$\frac{1}{2}$)2>0,
∴p>0.5.
故选:C.
点评 本题考查两个数值大小关系的判断,是基础题,解题时要认真审题,注意概率性质、作差法的合理运用.

练习册系列答案
相关题目
14.某学校采用系统抽样方法,从该校高一年级全体800名学生中抽50名学生做视力检查,现将800名学生从1到800进行编号.已知从1-16这16个数中被抽到的数是11,则编号在33-48中被抽到的数是( )
| A. | 39 | B. | 41 | C. | 43 | D. | 45 |
15.已知数列{an}中,a1=1,若an+1=3an+2(n∈N*),则数列{an}的通项公式an=( )
| A. | 2×3n-1 | B. | 2×3n-1-1 | C. | 2×3n-1+1 | D. | 3×2n-1-2 |
12.已知函数f(x)=3x2+2ax-a2,其中a∈(0,3],f(x)≤0对任意的x∈[-1,1]都成立,在1和a两数间插入2015个数,使之与1,a构成等比数列,设插入的这2015个数的乘积为T,则T=( )
| A. | 22015 | B. | 32015 | C. | ${3}^{\frac{2015}{2}}$ | D. | ${2}^{\frac{2015}{2}}$ |
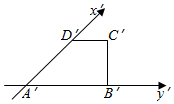 如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.
如图,四边形A′B′C′D′是直角梯形,它是四边形ABCD水平放置时的直观图,下底A′B′=20,上底C′D′=10,垂直于底的腰B′C′=10,求B′C′在原平面图形ABCD中的对应线段BC的长度.