题目内容
8.已知0<x<$\frac{3}{2}$,则y=$\frac{2}{x}$+$\frac{9}{3-2x}$的最小值为25.分析 由题意可得0<3-2x<3,整体代入变形可得y=$\frac{4}{2x}$+$\frac{9}{3-2x}$=($\frac{4}{2x}$+$\frac{9}{3-2x}$)[2x+(3-2x)]=13+$\frac{4(3-2x)}{2x}$+$\frac{18x}{3-2x}$,由基本不等式可得.
解答 解:∵0<x<$\frac{3}{2}$,∴0<3-2x<3,
∴y=$\frac{2}{x}$+$\frac{9}{3-2x}$=$\frac{4}{2x}$+$\frac{9}{3-2x}$=($\frac{4}{2x}$+$\frac{9}{3-2x}$)[2x+(3-2x)]
=13+$\frac{4(3-2x)}{2x}$+$\frac{18x}{3-2x}$≥13+2$\sqrt{\frac{4(3-2x)}{2x}•\frac{18x}{3-2x}}$=25
当且仅当$\frac{4(3-2x)}{2x}$=$\frac{18x}{3-2x}$即x=$\frac{3}{5}$时取等号.
故答案为:25.
点评 本题考查基本不等式求最值,整体变形为可用基本不等式的形式是解决问题的关键,属基础题.

练习册系列答案
相关题目
3.若不等式3sin2x-cos2x+4cosx+a≥-4对一切x都成立,则实数a的取值范围为( )
| A. | (1,+∞) | B. | (-1,+∞) | C. | [1,+∞) | D. | [-1,+∞) |
8.已知函数$f(x)={2^x}+\frac{1}{4}x-5$,则f(x)的零点所在的区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
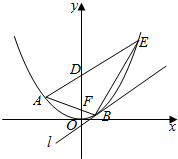 如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l
如图AB是抛物线C:x2=4y过焦点F的弦(点A在第二象限),过点A的直线交抛物线于点E,交y轴于点D(D在F上方),且|AF|=|DF|,过点B作抛物线C的切线l