题目内容
12.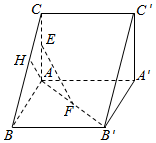 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC⊥AB,E,F,H分别是AC,AB′,BC的中点.
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC⊥AB,E,F,H分别是AC,AB′,BC的中点.(1)证明:EF⊥AH
(2)求四面体E-FAH的体积.
分析 (1)连结B′C.由中位线定理得EF∥B′C,由AB=AC得AH⊥BC,由BB′⊥平面ABC得BB′⊥AH,故AH⊥平面BB′C,于是AH⊥B′C,从而EF⊥AH;
(2)过F作FM⊥AB于M,则FM⊥平面ABC,求出FM和S△AEH,于是VE-FAH=VF-AEH.
解答 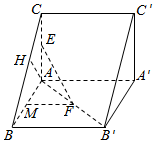 证明:(1)连结B′C.
证明:(1)连结B′C.
∵E,F分别是AC,AB′的中点,
∴EF∥B′C,
∵AB=AC,H是BC的中点,∴AH⊥BC,
∵BB′⊥平面ABC,AH?平面ABC,
∴BB′⊥AH,又BC?平面BB′C,BC?平面BB′C,BB′∩BC=B,
∴AH⊥平面BB′C,∵B′C?平面BB′C,
∴AH⊥B′C,又B′C∥EF,
∴EF⊥AH.
解:(2)过F作FM⊥AB于M,则FM⊥平面ABC,FM=$\frac{1}{2}$BB′=1.
∵S△AEH=$\frac{1}{2}AE•EH$=$\frac{1}{2}$,
∴VE-FAH=VF-AEH=$\frac{1}{3}{S}_{△AEH}•FM$=$\frac{1}{3}×\frac{1}{2}×1$=$\frac{1}{6}$.
点评 本题考查了线面垂直的判定与性质,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
20.(2x2+3x+1)6的展开式中,x2的系数是( )
| A. | 72 | B. | 147 | C. | 132 | D. | 75 |
3.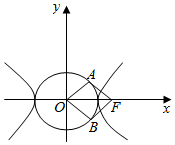 已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )
已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )
 已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )
已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
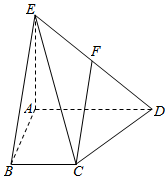 四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.
四棱锥E-ABCD中,AD∥BC,AD=AE=2BC=2AB=2,AB⊥AD,平面EAD⊥平面ABCD,点F为DE的中点.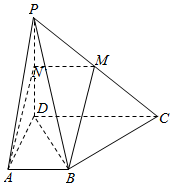 已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,∠DAB=90°,PD⊥底面ABCD,且PD=DA=CD=2AB=2,M为PC的中点,过A,B,M三点的平面与PD交于点N.
已知四棱锥P-ABCD的底面是直角梯形,AB∥CD,∠DAB=90°,PD⊥底面ABCD,且PD=DA=CD=2AB=2,M为PC的中点,过A,B,M三点的平面与PD交于点N.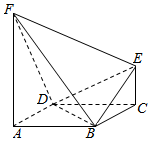 如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE.
如图,在几何体ABCDEF中,FA⊥平面ABCD,EC∥FA,FA=2EC=2$\sqrt{2}$,底面ABCD为平行四边形,AD⊥BD,AD=BD=2,FD⊥BE. 如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且$\frac{SE}{EC}$=$\frac{SF}{FD}$=$\frac{AG}{GC}$.
如图所示,四棱锥S-ABCD中,底面ABCD为正方形,且AB=4,SA⊥平面ABCD,∠SDA=60°,E、F、G分别是SC、SD、AC上的点,且$\frac{SE}{EC}$=$\frac{SF}{FD}$=$\frac{AG}{GC}$.