题目内容
17．（1）求与椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$有相同的焦点，且经过点（4，3）的椭圆的标准方程．（2）求与双曲线$\frac{x^2}{4}-\frac{y^2}{9}=1$有相同的渐近线，且焦距为$2\sqrt{13}$的双曲线的标准方程．
分析 （1）由题意可设椭圆方程$\frac{x^2}{16+λ}+\frac{y^2}{9+λ}=1（{λ＞-9}）$，代入（4，3），解方程可得λ，进而得到所求椭圆方程；
（2）由题意可设所求双曲线的方程为$\frac{{x}^{2}}{4λ}$-$\frac{{y}^{2}}{9λ}$=1（λ≠0），由焦距可得4|λ|+9|λ|=13，解方程即可得到所求双曲线的方程．
解答 解：（1）由所求椭圆与椭圆$\frac{x^2}{16}+\frac{y^2}{9}=1$有相同的焦点，
设椭圆方程$\frac{x^2}{16+λ}+\frac{y^2}{9+λ}=1（{λ＞-9}）$，
由（4，3）在椭圆上得$\frac{16}{16+λ}+\frac{9}{9+λ}=1⇒λ=12$，
则椭圆方程为$\frac{x^2}{28}+\frac{y^2}{21}=1$；
（2）由双曲线$\frac{x^2}{4}-\frac{y^2}{9}=1$有相同的渐近线，
设所求双曲线的方程为$\frac{{x}^{2}}{4λ}$-$\frac{{y}^{2}}{9λ}$=1（λ≠0），
由题意可得c2=4|λ|+9|λ|=13，
解得λ=±1．
即有双曲线的方程为$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{9}$=1或$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{4}$=1．
点评 本题考查相同焦点的椭圆方程的求法，以及相同渐近线方程的双曲线方程的求法，注意运用待定系数法，考查运算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
8．已知椭圆C1：$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1（{a_1}＞{b_1}＞0）$与双曲线C2：$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1（{a_2}＞0，{b_2}＞0）$有相同的焦点F1，F2，点P是两曲线的一个公共点，且PF1⊥PF2，e1，e2分别是两曲线C1，C2的离心率，当4e12+e22取得最小值时，C1的离心率e1等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{3}$ |
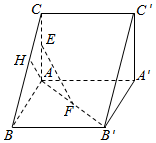如图所示，已知直三棱柱ABC-A′B′C′，AC=AB=AA′=2，AC⊥AB，E，F，H分别是AC，AB′，BC的中点．
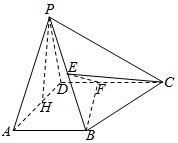如图所示，在四棱锥P-ABCD中，AB⊥平面PAD，AB∥CD，PD=AD，E是PB的中点，F是DC上的点且DF=$\frac{1}{2}$AB，PH为△PAD中AD边上的高．