题目内容
4．在平面直角坐标系xOy，已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的一个渐近线的方程为y=$\sqrt{3}$x，则该双曲线的离心率为2．分析 求出双曲线的渐近线方程y=±$\frac{b}{a}$x，由题意可得b=$\sqrt{3}$a，由a，b，c的关系和离心率公式计算即可得到所求值．
解答 解：双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的渐近线方程为y=±$\frac{b}{a}$x，
由一条渐近线的方程为y=$\sqrt{3}$x，可得b=$\sqrt{3}$a，
即有c=$\sqrt{{a}^{2}+{b}^{2}}$=2a，
即有e=$\frac{c}{a}$=2．
故答案为：2．
点评 本题考查双曲线的离心率的求法，注意运用渐近线方程和基本量的关系，考查运算能力，属于基础题．
练习册系列答案
相关题目
15．设f（x）=|ln（x+1）|，已知f（a）=f（b）（a＜b），则（ ）
| A． | a+b＞0 | B． | a+b＞1 | C． | 2a+b＞0 | D． | 2a+b＞1 |
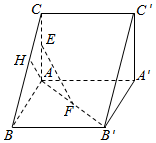如图所示，已知直三棱柱ABC-A′B′C′，AC=AB=AA′=2，AC⊥AB，E，F，H分别是AC，AB′，BC的中点．
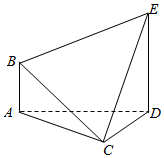在如图所示的多面体ABCDE中，AB⊥平面ACD，DE⊥平面ACD，AB=CD=1，AC=$\sqrt{3}$，AD=DE=2．