题目内容
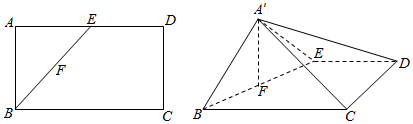
20．
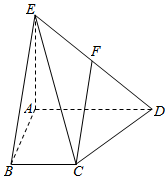四棱锥E-ABCD中，AD∥BC，AD=AE=2BC=2AB=2，AB⊥AD，平面EAD⊥平面ABCD，点F为DE的中点．（Ⅰ）求证：CF∥平面EAB；
（Ⅱ）若CF⊥AD，求四棱锥E-ABCD的体积．
分析 （1）取AE中点G，连接GF，GB，则EF$\stackrel{∥}{=}\frac{1}{2}AD\stackrel{∥}{=}BC$，故四边形BCFG是平行四边形，于是CF∥BG，得出CF∥平面EAB；
（2）由CF⊥AD得出BG⊥AD，又AB⊥AD，故AD⊥平面EAB，于是AD⊥EA，由面面垂直的性质得出EA⊥平面ABCD，即EA棱锥E-ABCD的高．
解答 
证明：（I）取AE中点G，连接GF，GB，
∵F是ED的中点，
∴GF$\stackrel{∥}{=}$$\frac{1}{2}$AD，
有∵BC$\stackrel{∥}{=}$$\frac{1}{2}$AD，
∴GF$\stackrel{∥}{=}BC$，
∴四边形BCFG是平行四边形，
∴GB∥CF，又BG?平面EAB，CF?平面EAB，
∴CF∥平面EAB，
（2）∵CF⊥AD，CF∥BG，
∴BG⊥AD，又AB⊥AD，BG?平面EAB，AB?平面EAB，BG∩AB=B，
∴AD⊥平面EAB，∵EA?平面AEB，
∴AD⊥EA，
又平面EAD⊥平面ABCD，平面EAD∩平面ABCD=AD，EA?平面EAD，
∴EA⊥平面ABCD，
∴VE-ABCD=$\frac{1}{3}{S}_{梯形ABCD}•EA$=$\frac{1}{3}×\frac{1}{2}×（1+2）×1×2$=1．
点评 本题考查了线面平行的判定，面面垂直的性质，棱锥的体积计算，属于中档题．
练习册系列答案
相关题目
8．已知sinθ=$\frac{m-3}{m+5}$，cosθ=$\frac{4-2m}{m+5}$，其中$\frac{π}{2}$＜θ＜π，则tanθ=（ ）
| A． | -$\sqrt{2}$ | B． | -$\frac{12}{5}$ | C． | -2 | D． | -$\frac{5}{12}$ |
8．已知椭圆C1：$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1（{a_1}＞{b_1}＞0）$与双曲线C2：$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1（{a_2}＞0，{b_2}＞0）$有相同的焦点F1，F2，点P是两曲线的一个公共点，且PF1⊥PF2，e1，e2分别是两曲线C1，C2的离心率，当4e12+e22取得最小值时，C1的离心率e1等于（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{3}$ |
15．设f（x）=|ln（x+1）|，已知f（a）=f（b）（a＜b），则（ ）
| A． | a+b＞0 | B． | a+b＞1 | C． | 2a+b＞0 | D． | 2a+b＞1 |
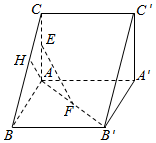如图所示，已知直三棱柱ABC-A′B′C′，AC=AB=AA′=2，AC⊥AB，E，F，H分别是AC，AB′，BC的中点．