题目内容
3.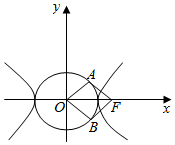 已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )
已知双曲线方程$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$,以O为圆心,实半轴长为半径作圆O,过双曲线的焦点F作圆O的两条切线,切点为A,B,若四边形FAOB为正方形,则双曲线的离心率为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 求得圆O的方程,由正方形的性质可得对角线OF的长为$\sqrt{2}$a,再由离心率公式计算即可得到所求值.
解答 解:由题意可得圆O的方程为x2+y2=a2,
由四边形FAOB为边长为a的正方形,
可得对角线OF的长为$\sqrt{2}$a,
即有c=$\sqrt{2}$a,
则离心率e=$\frac{c}{a}$=$\sqrt{2}$.
故选:B.
点评 本题考查双曲线的离心率的求法,注意运用直线和圆相切的性质和正方形的性质,考查运算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.已知椭圆C1:$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1({a_1}>{b_1}>0)$与双曲线C2:$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1({a_2}>0,{b_2}>0)$有相同的焦点F1,F2,点P是两曲线的一个公共点,且PF1⊥PF2,e1,e2分别是两曲线C1,C2的离心率,当4e12+e22取得最小值时,C1的离心率e1等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{3}$ |
15.设f(x)=|ln(x+1)|,已知f(a)=f(b)(a<b),则( )
| A. | a+b>0 | B. | a+b>1 | C. | 2a+b>0 | D. | 2a+b>1 |
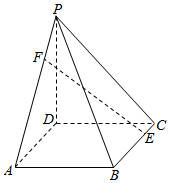 如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.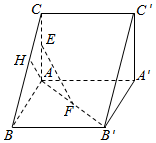 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC⊥AB,E,F,H分别是AC,AB′,BC的中点.
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC⊥AB,E,F,H分别是AC,AB′,BC的中点.