已知a∈R.则复数(a2+a+1)-(a2-2a+3)i对应的点在复平面内的第四象限．题目和参考答案——青夏教育精英家教网—

题目内容

20．已知a∈R，则复数（a²+a+1）-（a²-2a+3）i对应的点在复平面内的第四象限．

分析配方可判实部和虚部的正负，由复数的几何意义可得．

解答解：∵a∈R，∴a²+a+1=（a+$\frac{1}{2}$）²+$\frac{3}{4}$＞0，
同理可得-（a²-2a+3）=-（a-1）²-2＜0，
∴已知复数对应的点在复平面内的第四象限，
故答案为：四．

点评本题考查复数的代数形式和复数的几何意义，属基础题．

练习册系列答案

相关题目

10．

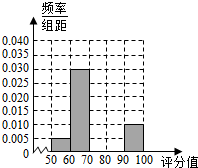某地有2000名学生参加数学学业水平考试，现将成绩（满分：100分）汇总，得到如图所示的频率分布表．
（1）请完成题目中的频率分布表，并补全题目中的频率分布直方图；

成绩分组	频数	频率
[50，60]	100
（60，70]
（70，80]	800
（80，90]
（90，100]	200

（2）将成绩按分层抽样的方法抽取150名同学进行问卷调查，甲同学在本次测试中数学成绩为95分，求他被抽中的概率．

11．设0＜a＜b，则下列不等式中正确的是（　　）

A．

a＜b＜$\sqrt{ab}$＜$\frac{a+b}{2}$

B．

a＜$\sqrt{ab}$＜$\frac{a+b}{2}$＜b

C．

a＜$\sqrt{ab}$＜b＜$\frac{a+b}{2}$

D．

$\sqrt{ab}$＜a＜$\frac{a+b}{2}$＜b

8．已知等腰△ABC的底边AB所在的直线方程为$\sqrt{3}$x-y+2=0，顶点C的坐标是（2，2），顶角为120°，求两腰所在的直线方程及△ABC的面积．

15．已知函数f（x）=$\frac{1}{a}$-$\frac{1}{x}$（a＞0，x＞0）．
（1）求证：f（x）在（0，+∞）上是单调递增函数；
（2）若f（x）在[$\frac{1}{2}$，2]上的值域是[$\frac{1}{2}$，2]，求a的值；
（3）若存在正数m，n使得f（x）在[m，n]上的值域为[4m+1，4n+1]，求a的取值范围．

5．解方程：
（1）6^2x+4=3^3x×2^x+8；
（2）5^x+1=3${\;}^{{x}^{2}-1}$．

12．已知函数f（x）=-x²+2x．则不等式f（log₂x）＜f（2）的解集为（4，+∞）∪（0，1）．

9．已知点D，E分别为△ABC边AB，AC的中点，F为DE的中点．则$\overrightarrow{BF}$=（　　）

A．

$\frac{5}{6}\overrightarrow{BE}$+$\frac{1}{6}$$\overrightarrow{DC}$

B．

$\frac{5}{6}$$\overrightarrow{BE}$+$\frac{1}{3}$$\overrightarrow{DC}$

C．

$\frac{5}{6}$$\overrightarrow{BE}$$-\frac{1}{6}$$\overrightarrow{DC}$

D．

$\frac{5}{6}$$\overrightarrow{BE}$$-\frac{1}{3}$$\overrightarrow{DC}$

15．

函数f（x）的图象为如图所示的折线段ABC，设g（x）=$\frac{lo{g}_{3}x}{f（x）}$，则函数g（x）的最大值为（　　）

试题分类