题目内容
若椭圆焦点在x轴上且经过点（-4，0），c=3，其焦点在x轴上，则该椭圆的标准方程为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设出椭圆的标准方程，根据题意求出a、b的值，即得椭圆的标准方程．
解答：
解：设椭圆的标准方程为
+
=1（a＞b＞0），
根据题意得，
=1，∴a=4；
又∵a2=b2+c2，
∴b2=42-32=7；
∴椭圆的标准方程为
+
=1．
故选：B．
| x2 |
| a2 |
| y2 |
| b2 |
根据题意得，
| (-4)2 |
| a2 |
又∵a2=b2+c2，
∴b2=42-32=7；
∴椭圆的标准方程为
| x2 |
| 16 |
| y2 |
| 7 |
故选：B．
点评：本题考查了求椭圆的标准方程的问题，解题时应先设出椭圆的标准方程，根据题意，求出椭圆的标准方程来，是基础题．
练习册系列答案
相关题目
已知方程|x2-a|-x+2=0（a＞0）有两个不等的实数根，则实数a的取值范围是（ ）
| A、0＜a＜4 | B、a＞4 |
| C、0＜a＜2 | D、a＞2 |
函数f（x）=ex-x-2（e≈2.72）的一个零点所在的区间是（ ）
| A、（1，2） |
| B、（0，1） |
| C、（-1，0） |
| D、（2，3） |
设P是椭圆
+
=1上一点，F1、F2是椭圆的焦点，若|PF1|等于4，则|PF2|等于（ ）
| x2 |
| 169 |
| y2 |
| 25 |
| A、22 | B、21 | C、20 | D、13 |
已知函数f（x）=x2+bx+c，其中0≤b≤4，0≤c≤4，记函数f（x）满足条件：f（2）≤12为事件A，则事件A发生的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f（x）对?x∈R满足f（x）=-f（2-x），且在[1，+∞）上递增，若g（x）=f（1+x），且2g（log2a）-3g（1）≤g（log
a），则实数a的范围为（ ）
| 1 |
| 2 |
| A、（0，2] | ||
B、（0，
| ||
C、[
| ||
| D、[1，2] |
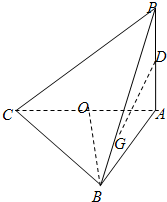如图，在三棱锥P-ABC中，PA⊥平面ABC，AB⊥AC．