Question

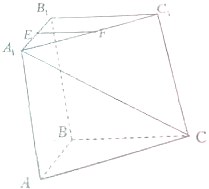已知如图，在直三棱柱ABC-A₁B₁C₁中（侧棱垂直底面内所有直线的棱柱叫做
直棱柱），AA₁=

2

，AB=BC=1，∠ABC=90°，E、F分别是A₁B₁、A₁C₁的中点．
（1）求线段A₁C的大小；
（2）求异面直线A₁C与EF所成的角的大小．

Answer 1

考点：异面直线及其所成的角

专题：空间位置关系与距离

分析：（1）根据几何性质，得出四边形AA₁C₁C为正方形，即可求解，（2）根据直线的平行得出∠A₁CB为异面直线A₁C与EF所成的角，求出边长，利用直角三角形即可求解．

解答： 解：（1）∵在直三棱柱ABC-A₁B₁C₁中AA₁=

2

，AB=BC=1，∠ABC=90°，
∴可知四边形AA₁C₁C为正方形，AB=

2

，
∴A₁C=

2+2

=2，
（2）∵E、F分别是A₁B₁、A₁C₁的中点，
∴EF∥B₁C₁，
∵B₁C₁∥BC，
∴∠A₁CB为异面直线A₁C与EF所成的角，
△∴A₁CB中，AA₁=

2

，A₁B=

3

，BC=1，
A₁C=2，
∴可判断为直角三角形，
sin∠A₁CB=

A1B

A1C

=

3

2

，
∴∠A₁CB为60°
故异面直线A₁C与EF所成的角为60°．

点评：本题考查了空间几何体的性质，运用求解线段的长度，夹角，属于计算题，难度不大．