题目内容
利用单位圆中的三角函数线,确定下列各角的取值范围.
(1)-1≤sinθ≤
;
(2)sinθ<cosθ.
(1)-1≤sinθ≤
| 1 |
| 2 |
(2)sinθ<cosθ.
考点:三角函数线
专题:数形结合,三角函数的图像与性质
分析:(1)首先在[0,2π]范围内找到三角函数线为-1,
的角度,然后再由终边相同角写出集合.
(2)首先在[0,2π]范围内找到三角函数线为OM>BM的θ的角度,然后再由终边相同角写出集合.
| 1 |
| 2 |
(2)首先在[0,2π]范围内找到三角函数线为OM>BM的θ的角度,然后再由终边相同角写出集合.
解答:
解:如图所示:在直角坐标系中,作出单位圆,把角θ的顶放到原点,角的始边放到x轴的正半轴上.
设θ的终边与单位圆的交点为B,单位圆和x轴的正半轴的交点为A,再作BM⊥x轴,M为垂足,则有BM=sinθ,OM=cosθ,OA=1.

(1)在单位圆中-1≤sinθ≤
时的在[0,2π]的角度是0≤θ≤
,或
≤θ≤2π,
所以θ取值范围为:2kπ≤θ≤
+2kπ,或2kπ+
≤θ≤2kπ+2π,k∈Z.
(2)在单位圆中sinθ<cosθ时的在[0,2π]的角度是
<θ≤2π,或0≤θ<
,
所以θ取值范围为:2kπ+
<θ≤2π+2kπ,或2π≤θ<2kπ+
,k∈Z.
设θ的终边与单位圆的交点为B,单位圆和x轴的正半轴的交点为A,再作BM⊥x轴,M为垂足,则有BM=sinθ,OM=cosθ,OA=1.

(1)在单位圆中-1≤sinθ≤
| 1 |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
所以θ取值范围为:2kπ≤θ≤
| π |
| 6 |
| 5π |
| 6 |
(2)在单位圆中sinθ<cosθ时的在[0,2π]的角度是
| 5π |
| 4 |
| π |
| 4 |
所以θ取值范围为:2kπ+
| 5π |
| 4 |
| π |
| 4 |
点评:本题考查了三角函数线的运用求满足条件的角的集合,属于基础题.

练习册系列答案
相关题目
“ab=0”是“a=0且b=0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
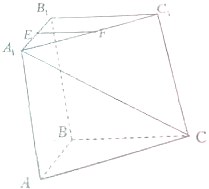 已知如图,在直三棱柱ABC-A1B1C1中(侧棱垂直底面内所有直线的棱柱叫做
已知如图,在直三棱柱ABC-A1B1C1中(侧棱垂直底面内所有直线的棱柱叫做