题目内容
函数f(x)=
，若互不相等的实数x1，x2，x3满足f（x1）=f（x2）=f（x3），则x1+x2+x3的取值范围为（ ）
|
| A、（-5，4] |
| B、（-5，3） |
| C、（-1，4） |
| D、（-1，3] |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：先画出函数的图象，得到x2+x3的值，求出x1的取值范围，从而得到答案．
解答：
解：画出函数f（x）的图象，如图示：
，
不妨设则x1＜x2＜x3，则x2+x3=4，-5＜x1≤-1，
∴-1＜x1+x2+x3≤3，
故选：D．
，不妨设则x1＜x2＜x3，则x2+x3=4，-5＜x1≤-1，
∴-1＜x1+x2+x3≤3，
故选：D．
点评：本题考查了函数的零点问题，考查了函数的对称性，是一道中档题．
练习册系列答案
相关题目
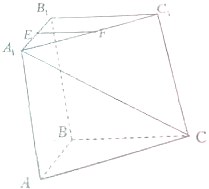已知如图，在直三棱柱ABC-A1B1C1中（侧棱垂直底面内所有直线的棱柱叫做