题目内容
已知数列{an}的前n项和Sn满足Sn+1=(k+1)Sn+2,又a1=2,a2=1.
(1)求实数k的值;
(2)问数列{an}是等比数列吗?若是,给出证明;若不是,说明理由;
(3)求出数列{an}的前n项和Sn.
(1)求实数k的值;
(2)问数列{an}是等比数列吗?若是,给出证明;若不是,说明理由;
(3)求出数列{an}的前n项和Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件推导出a1+a2=(k+1)a1+2.由a1=2,a2=1,能求出k的值.
(2)数列{an}是等比数列.由(1)知Sn+1=
Sn+2,由此推导出an+1=
an(n≥2),由此能证明数列{an}是等比数列.
(3)由(2)知等比数列{an}中,a1=2,q=
,由此能求出数列{an}的前n项和Sn.
(2)数列{an}是等比数列.由(1)知Sn+1=
| 1 |
| 2 |
| 1 |
| 2 |
(3)由(2)知等比数列{an}中,a1=2,q=
| 1 |
| 2 |
解答:
解:(1)∵Sn+1=(k+1)Sn+2,∴S2=(k+1)S1+2,
∴a1+a2=(k+1)a1+2.…(2分)
又∵a1=2,a2=1,∴2+1=2(k+1)+2,
解得k=-
.…(4分)
(2)数列{an}是等比数列.…(5分)
由(1)知Sn+1=
Sn+2,①
当n≥2时,Sn=
Sn-1+2,②
①-②得an+1=
an(n≥2).…(7分)
又∵a2=
a1,且an≠0(n∈N*),
∴
=
(n∈N*),
∴数列{an}是等比数列,公比为
,
∴an=a1qn-1=2×(
)n-1=
.…(9分)
(3)∵a1=2,q=
,
∴Sn=
=4(1-
).…(12分)
∴a1+a2=(k+1)a1+2.…(2分)
又∵a1=2,a2=1,∴2+1=2(k+1)+2,
解得k=-
| 1 |
| 2 |
(2)数列{an}是等比数列.…(5分)
由(1)知Sn+1=
| 1 |
| 2 |
当n≥2时,Sn=
| 1 |
| 2 |
①-②得an+1=
| 1 |
| 2 |
又∵a2=
| 1 |
| 2 |
∴
| an+1 |
| an |
| 1 |
| 2 |
∴数列{an}是等比数列,公比为
| 1 |
| 2 |
∴an=a1qn-1=2×(
| 1 |
| 2 |
| 1 |
| 2n-2 |
(3)∵a1=2,q=
| 1 |
| 2 |
∴Sn=
2[1-(
| ||
1-
|
| 1 |
| 2n |
点评:本题考查数列中参数的求法,考查等比数列的判断与证明,考查数列的前n项和的求法,是中档题,解题时要熟练掌握等比数列的性质.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
点P(x,y)为不等式组
表示的平面区域上一点,则x+2y取值范围为( )
|
A、[-
| ||||
B、[-2,
| ||||
| C、[-1,2] | ||||
| D、[-2,2] |
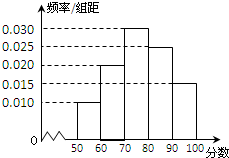 某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图的频率分布直方图.样本数据分组为[50,60),[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有( )
某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图的频率分布直方图.样本数据分组为[50,60),[60,70),[70,80),[80,90),[90,100].若用分层抽样的方法从样本中抽取分数在[80,100]范围内的数据16个,则其中分数在[90,100]范围内的样本数据有( )| A、5个 | B、6个 | C、8个 | D、10个 |
 如图为函数f(x)=Asin(ωx+φ)(其中ω>0,0≤φ≤
如图为函数f(x)=Asin(ωx+φ)(其中ω>0,0≤φ≤| π |
| 2 |
A、-
| ||||
B、-
| ||||
| C、-1 | ||||
| D、1 |
 正方体ABCD-A1B1C1D1的棱长为1,P为线段BC的中点,Q为线段CC1上的动点,过A,P,Q的平面截该正方体所得的截面记为S,则所有正确的命题是
正方体ABCD-A1B1C1D1的棱长为1,P为线段BC的中点,Q为线段CC1上的动点,过A,P,Q的平面截该正方体所得的截面记为S,则所有正确的命题是