题目内容
15.如图1,△ABC为等腰直角三角形,∠B=90°,将△ABC沿中位线DE翻折,得到如图2所示的空间图形(∠ADB为锐角).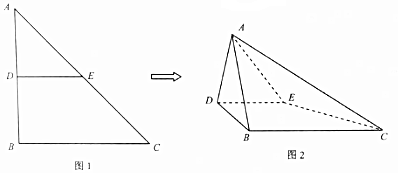
(1)求证:BC⊥平面ABD;
(2)若BC=2,当三棱锥A-BCE的体积为$\frac{\sqrt{3}}{6}$时,求∠ABD的大小.
分析 (1)证明:DE⊥平面ADB,DE∥BC,即可证明BC⊥平面ABD;
(2)求出A到平面BCE的距离,即可求∠ABD的大小.
解答 (1)证明:由题意,DE∥BC,
∵DE⊥AD,DE⊥BD,AD∩BD=D,
∴DE⊥平面ADB,
∴BC⊥平面ABD;
(2)解:由题意,S△BCE=$\frac{1}{2}×2×1$=1,
设A到平面BCE的距离为h,则$\frac{1}{3}×1×h$=$\frac{\sqrt{3}}{6}$,∴h=$\frac{\sqrt{3}}{2}$
∵AD=1,∴sin∠ABD=$\frac{\sqrt{3}}{2}$,∴∠ABD=60°.
点评 本题考查线面垂直,考查三棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
5.中心在坐标原点的双曲线C的两条渐近线与圆(x-2)2+y2=3相切,则双曲线的离心率为( )
| A. | 2 | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2或$\frac{2\sqrt{3}}{3}$ |
6. 某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
 某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )
某三棱锥的三视图如图所示,则该三棱锥的各个侧面中最大的侧面的面积为( )| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\sqrt{2}$ |
10.执行如图所示的程序框图,输出的x值为( )


| A. | 0 | B. | 3 | C. | 6 | D. | 8 |
7.已知函数f(x)在(-1,+∞)上单调,且函数y=f(x-2)的图象关于x=1对称,若数列{an}是公差不为0的等差数列,且f(a50)=f(a51),则{an}的前100项的和为( )
| A. | -200 | B. | -100 | C. | 0 | D. | -50 |
4.已知不等式组$\left\{\begin{array}{l}{x+y-3≥0,}&{\;}\\{x-2y+3≥0,}&{\;}\\{x≤a}&{\;}\end{array}\right.$,(a>1)表示的平面区域为D,点(x0,y0)在平面区域D上,则3x0-y0的最小值等于( )
| A. | 4a-3 | B. | -1 | C. | 1 | D. | $\frac{5a-3}{2}$ |
5.已知直线l过定点(0,1),则“直线l与圆(x-2)2+y2=4相切”是“直线l的斜率为$\frac{3}{4}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |