已知随机变量X服从正态分布N=0.6826.则P(附:若随机变量ξ服从正态分布N(μ.σ2).且P=68.26%.P=95.44%)A．0.1588B．0.1587C．0.1586D．0.1585 题目和参考答案——青夏教育精英家教网—

题目内容

12．已知随机变量X服从正态分布N（3，1），且P（2≤X≤4）=0.6826，则P（X＞4）等于（　　）
（附：若随机变量ξ服从正态分布N（μ，σ²），且P（μ-σ＜ξ＜μ+σ）=68.26%，P（μ-2σ＜ξ＜μ+2σ）=95.44%）

A．

0.1588

B．

0.1587

C．

0.1586

D．

0.1585

分析根据随机变量X服从正态分布，可知正态曲线的对称轴，利用对称性，即可求得P（X＞4）．

解答解：∵随机变量X服从正态分布N（3，1），
∴正态曲线的对称轴是x=3，
∵P（2≤X≤4）=0.6826，
∴P（X＞4）=0.5-$\frac{1}{2}$P（2≤X≤4）=0.5-0.3413=0.1587．
故选：B．

点评本题主要考查正态分布曲线的特点及曲线所表示的意义，注意根据正态曲线的对称性解决问题．

练习册系列答案

3．在直二面角α-l-β中，线段AB的端点A，B分别在α，β内，且AB与α，β所成的角均为30°，则AB与l所成的角为（　　）

20．

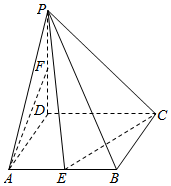如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠DAB=60°，PD⊥平面ABCD，PD=AD=2，点E，F分别为AB和PD的中点．
（Ⅰ）求证：直线AF∥平面PEC；
（Ⅱ）求点F到平面PEC的距离．

7．计算：
（1）求y=2$\sqrt{x}$-sin$\frac{x}{2}$cos$\frac{x}{2}$-e^-x的导数．
（2）${∫}_{0}^{4}$|x-2|dx．

17．已知α是第四象限角，且f（α）=$\frac{sin（-α-π）cos（5π-α）tan（4π-α）}{cos（\frac{5π}{2}-α）tan（-α-π）}$
（1）化简f（α）；
（2）若tan（α-π）=-3，求f（α）的值．

4．cos$\frac{11}{4}$π的值为（　　）

-$\frac{\sqrt{2}}{2}$

1．已知$\overrightarrow{AB}$=$\overrightarrow a$-7$\overrightarrow b$，$\overrightarrow{BC}$=-2$\overrightarrow{a}$+8$\overrightarrow{b}$，$\overrightarrow{CD}$=3（$\overrightarrow{a}$-$\overrightarrow{b}$），则（　　）

2．

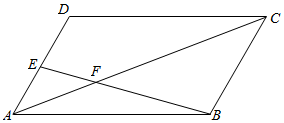如图，E是平行四边形ABCD的边AD上一点，且$\overrightarrow{AE}$=$\frac{1}{4}$$\overrightarrow{AD}$，F为BE与AC的交点，设$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{BC}$=$\overrightarrow{b}$，若$\overrightarrow{BF}$=k$\overrightarrow{BE}$，$\overrightarrow{AF}$=h$\overrightarrow{AC}$，则k=$\frac{4}{5}$，h=$\frac{1}{5}$．

试题分类