题目内容
17.已知α是第四象限角,且f(α)=$\frac{sin(-α-π)cos(5π-α)tan(4π-α)}{cos(\frac{5π}{2}-α)tan(-α-π)}$(1)化简f(α);
(2)若tan(α-π)=-3,求f(α)的值.
分析 (1)利用诱导公式化简求解函数的解析式即可.
(2)求出正切函数值,然后利用同角三角函数基本关系式求解即可.
解答 解:(1)f(α)=$\frac{sin(-α-π)cos(5π-α)tan(4π-α)}{cos(\frac{5π}{2}-α)tan(-α-π)}$=$\frac{sinαcosαtanα}{-sinαtanα}$=-cosα.
(2)tan(α-π)=-3,可得tanα=-3.$\left\{\begin{array}{l}{\frac{sinα}{cosα}=-3}\\{si{n}^{2}α+co{s}^{2}α=1}\end{array}\right.$,
可得cos2$α=\frac{1}{10}$,
α是第四象限角,
∴cosα=$\frac{\sqrt{10}}{10}$.
f(α)=-$\frac{\sqrt{10}}{10}$.
点评 本题考查诱导公式的应用,同角三角函数基本关系式的应用,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知球O的半径为1,A,B,C三点都在球面上,且∠AOB=∠AOC=∠BOC=90°,则球心O到平面ABC的距离为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
12.已知随机变量X服从正态分布N(3,1),且P(2≤X≤4)=0.6826,则P(X>4)等于( )
(附:若随机变量ξ服从正态分布N(μ,σ2),且P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
(附:若随机变量ξ服从正态分布N(μ,σ2),且P(μ-σ<ξ<μ+σ)=68.26%,P(μ-2σ<ξ<μ+2σ)=95.44%)
| A. | 0.1588 | B. | 0.1587 | C. | 0.1586 | D. | 0.1585 |
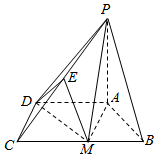 已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.
已知四棱锥P-ABCD,底面ABCD是直角梯形,AD∥BC,∠BCD=90°,PA⊥底面ABCD,△ABM是边长为2的等边三角形,$PA=DM=2\sqrt{3}$.