题目内容
7.画出方程x4-x2=y4-y2的曲线C,并回答下列问题:(1)若点A(m,$\sqrt{2}$)在曲线C上,求m的值;
(2)若直线y=a(a∈R)与曲线C分别有一个、两个、三个、四个交点,求a的取值范围.
分析 (1)点A(m,$\sqrt{2}$)在曲线C上,代入方程,即可求m的值;
(2)解方程组$\left\{\begin{array}{l}{y=±x}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$得直线与圆的四个交点A($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),B(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),E($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),D(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),结合图象,求a的取值范围.
解答 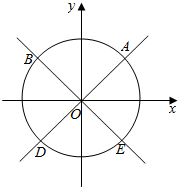 解:原方程可化为(x2-y2)(x2+y2-1)=0即 y=±x或x2+y2=1.故方程的曲线C如图所示
解:原方程可化为(x2-y2)(x2+y2-1)=0即 y=±x或x2+y2=1.故方程的曲线C如图所示
(1)∵点A(m,$\sqrt{2}$)在曲 线C上,
∴(m2-2)[m2+($\sqrt{2}$)2-1]=0,
解之,有m=±$\sqrt{2}$.
(2)解方程组$\left\{\begin{array}{l}{y=±x}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$得直线与圆的四个交点A($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),B(-$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$),E($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),D(-$\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),结合图象可知:
当直线y=a与曲线C有两个交点时:
a>1或a<-1,或a=$\frac{\sqrt{2}}{2}$或a=-$\frac{\sqrt{2}}{2}$,
当直线y=a与曲线C有三个交点时:
a=1或a=-1,或a=0,
当直线y=a与曲线C有四个交点时:
0<a<1且a≠$\frac{\sqrt{2}}{2}$,或-1<a<0且a≠-$\frac{\sqrt{2}}{2}$,
由曲线的对称性知,直线y=a与曲线C不会只有一个交点,即不存在实数a,使直线y=a与曲线C有一个交点.
点评 本题考查曲线与方程,考查直线与圆的位置关系,考查数形结合的数学思想,属于中档题.

 名校课堂系列答案
名校课堂系列答案| A. | $±\frac{1}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{1}{3}$ | D. | ±$\frac{\sqrt{2}}{3}$ |
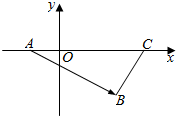 如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.
如图,在△ABC中,点A,C在x轴上,AB=4,∠BAC=30°,求向量$\overrightarrow{AB}$的坐标.