题目内容
已知抛物线的焦点F（a，0）（a＜0），则抛物线的标准方程是（ ）
| A、y2=2ax |
| B、y2=4ax |
| C、y2=-2ax |
| D、y2=-4ax |
考点：抛物线的标准方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：由焦点F（a，0）（a＜0），可设抛物线的方程为y2=-2px，由
=-a可求p，即可得出物线的标准方程．
| p |
| 2 |
解答：
解：由焦点F（a，0）（a＜0），可设抛物线的方程为y2=-2px
∵
=-a
∴p=-2a
∴y2=4ax
故选：B．
∵
| p |
| 2 |
∴p=-2a
∴y2=4ax
故选：B．
点评：本题主要考查了由抛物线的性质求解抛物线的方程，解题的关键是由抛物线的焦点确定抛物线的开口方向，属于基础试题．
练习册系列答案
相关题目
如图，设全集U=R，M={x|x＞2}，N={0，1，2，3}，则图中阴影部分所表示的集合是（ ）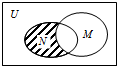
| A、{3} |
| B、{0，1} |
| C、{0，1，2} |
| D、{0，1，2，3} |
已知函数f（x）=Asin（ωx-| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|