已知扇形的半径是8cm.圆心角是45°的扇形所对的弧长是2πcm．题目和参考答案——青夏教育精英家教网——

题目内容

5．已知扇形的半径是8cm，圆心角是45°的扇形所对的弧长是2πcm．

分析先把圆心角化为弧度数，代入扇形的弧长公式：l=α•r 求出弧长．

解答解：圆心角为45°即$\frac{π}{4}$，由扇形的弧长公式得：弧长l=α•r=$\frac{π}{4}$•8=2πcm，
故答案为：2π．

点评本题考查弧长公式的应用，要注意公式中的圆心角一定要用弧度来表示，不能用度数，属于基础题．

练习册系列答案

课堂小作业系列答案

黄冈小状元口算速算练习册系列答案

成功训练计划系列答案

倍速训练法直通中考考点系列答案

浙江名卷系列答案

励耘活页系列答案

一卷搞定系列答案

名校作业本系列答案

提分教练系列答案

尖子生学案系列答案

相关题目

15．设实数x、y满足4x²-2$\sqrt{3}$xy+4y²=13，则x²+4y²的取值范围是$[10-4\sqrt{3}，10+4\sqrt{3}]$．

16．已知命题p：-x²+8x+20≥0；命题q：x²+2x+1-4m²≤0．
（1）当m∈R时，解不等式x²+2x+1-4m²≤0；
（2）当m＞0时，若￢p是￢q的必要不充分条件，求实数m的取值范围．

13．已知球的半径为4，相互垂直的两个平面分别截球面得两个圆，若两圆的公共弦长为4，则两圆的圆心距等于（　　）

20．执行如图所示的程序框图，则输出的结果是（　　）

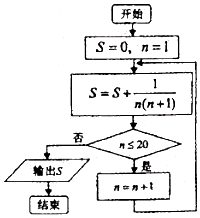
$\frac{21}{22}$

$\frac{20}{21}$

$\frac{19}{20}$

$\frac{22}{23}$

10．函数f（x）=2sin（x-$\frac{π}{4}$）在[0，2π]内的递减区间是[$\frac{3π}{4}$，$\frac{7π}{4}$]．

17．设θ∈（0，$\frac{π}{2}$），且cos（θ+$\frac{π}{6}$）=$\frac{1}{3}$．
（1）求sinθ的值；
（2）求sin（2θ+$\frac{π}{6}$）的值．

14．在平面直角坐标系中，曲线C₁：$\left\{\begin{array}{l}{x=3+3cosa}\\{y=2sina}\end{array}\right.$（a为参数）经过伸缩变换$\left\{\begin{array}{l}{x′=\frac{x}{3}}\\{y′=\frac{y}{2}}\end{array}\right.$后的曲线为C₂，以坐标原点为极点，x轴正半轴为极轴建立极坐标系．
（Ⅰ）求C₂的极坐标方程；
（Ⅱ）设曲线C₃的极坐标方程为ρsin（$\frac{π}{6}$-θ）=1，且曲线C₃与曲线C₂相交于P，Q两点，求|PQ|的值．

15．已知f（x）是R上的偶函数，且在[0，+∞）上单调递减，f（1）=0，则不等式f（x）＞0的解集为{x|-1＜x＜1}．