题目内容
3.已知向量$\overrightarrow{a}$与$\overrightarrow{b}$满足$\overrightarrow{a}$=(2,0),|$\overrightarrow{b}$|=1,若|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{7}$,则a与b的夹角是$\frac{π}{3}$.分析 对$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{7}$两边进行平方,根据条件进行数量积的运算即可得出$\overrightarrow{a}•\overrightarrow{b}$的值,进而得出向量$\overrightarrow{a},\overrightarrow{b}$的夹角.
解答 解:根据条件:
${\overrightarrow{a}}^{2}=4,{\overrightarrow{b}}^{2}=1$;
∴由$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{7}$得,$(\overrightarrow{a}+\overrightarrow{b})^{2}={\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=$4+2\overrightarrow{a}•\overrightarrow{b}+1=7$;
∴$\overrightarrow{a}•\overrightarrow{b}=1$;
∴$2•1•cos<\overrightarrow{a},\overrightarrow{b}>=1$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{1}{2}$;
∴$\overrightarrow{a},\overrightarrow{b}$的夹角为$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 考查根据向量坐标求向量长度的方法,向量数量积的运算及计算公式,已知三角函数值求角.

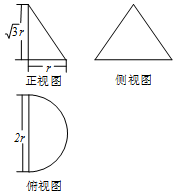 若一个空间几何体的三视图如图所示,且已知该几何体的体积为$\frac{\sqrt{3}}{6}π$,则其表面积为( )
若一个空间几何体的三视图如图所示,且已知该几何体的体积为$\frac{\sqrt{3}}{6}π$,则其表面积为( )| A. | $\frac{3}{2}π+\sqrt{3}$ | B. | $\frac{3}{2}π$ | C. | $\frac{3}{4}π+2\sqrt{3}$ | D. | $\frac{3}{4}π+\sqrt{3}$ |
| A. | 2 | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 4 |
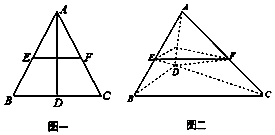 如图一,在边长为2的等边三角形ABC中,D、E、F分别是BC、AB、AC的中点,将△ABD沿AD折起,得到如图二所示的三棱锥A-BCD,其中$BC=\sqrt{2}$.
如图一,在边长为2的等边三角形ABC中,D、E、F分别是BC、AB、AC的中点,将△ABD沿AD折起,得到如图二所示的三棱锥A-BCD,其中$BC=\sqrt{2}$.