题目内容
已知数列{an}的首项a1=1,以后各项由公式an=
(n>1,n∈N*)给出,写出这个数列的前5项,并求该数列的通项公式.
| an-1 |
| an-1+1 |
考点:数列的概念及简单表示法,数列递推式
专题:等差数列与等比数列
分析:可根据递推公式写出数列的前5项,然后分析每一项与该项的序号之间的关系,归纳概括出an与n之间的一般规律,从而作出猜想,写出满足前5项的该数列的一个通项公式
解答:
解:∵an=
=
(n>1,n∈N*),a1=1,
∴a2=
=
,a3=
=
,a4=
=
,a5=
=
,
观察规律,
∴an=
| an-1 |
| an-1+1 |
| 1 | ||
1+
|
∴a2=
| 1 |
| 1+1 |
| 1 |
| 2 |
| 1 |
| 1+2 |
| 1 |
| 3 |
| 1 |
| 1+3 |
| 1 |
| 4 |
| 1 |
| 1+4 |
| 1 |
| 5 |
观察规律,
∴an=
| 1 |
| n |
点评:本题考查从特殊的事例,通过分析、归纳、抽象总结出一般规律,这是创新意识的具体体现,这种探索问题的方法,在解数列的有关问题中经常用到,应引起足够的重视

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
一个四面体的顶点在空间直角坐标系o-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的主视图时,以zox平面为投影面,则得到主视图可以为( )
A、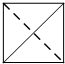 |
B、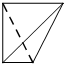 |
C、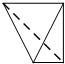 |
D、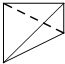 |
若双曲线
-
=1(a>0,b>0)的渐近线与圆(x-2)2+y2=1相切,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
若复数z的共轭复数为
,且满足
(2-i)=10+5i(i为虚数单位),则|z|=( )
. |
| z |
. |
| z |
| A、25 | ||
| B、10 | ||
| C、5 | ||
D、
|
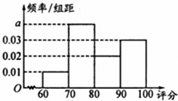 为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.
为检测某种零件的生产质量,检验人员抽取了同批次的零件作为样本进行检测并评分,若检测后评分结果大于60分的零件为合格零件.