题目内容
四面体ABCD的体积是
,△ABC是斜边AB=2的等腰直角三角形,若点A,B,C,D都在半径为
的同一球面上,则D与AB中点的距离是 .
| 1 |
| 6 |
| 2 |
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:设AB的中点为E,求出D到平面ABC的距离,球心到平面ABC的距离,即可得出结论.
解答:
 解:设AB的中点为E,则
解:设AB的中点为E,则
∵四面体ABCD的体积是
,△ABC是斜边AB=2的等腰直角三角形,
∴D到平面ABC的距离为DF=
,
∵点A,B,C,D都在半径为
的同一球面上,
∴球心到平面ABC的距离为OE=1,
如图所示,取OE的中点G,则DG⊥OE,
∴DE=OD=
.
故答案为:
.
 解:设AB的中点为E,则
解:设AB的中点为E,则∵四面体ABCD的体积是
| 1 |
| 6 |
∴D到平面ABC的距离为DF=
| 1 |
| 2 |
∵点A,B,C,D都在半径为
| 2 |
∴球心到平面ABC的距离为OE=1,
如图所示,取OE的中点G,则DG⊥OE,
∴DE=OD=
| 2 |
故答案为:
| 2 |
点评:本题考查几何体的体积,考查球,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
一个几何体的三视图如图所示,如该几何体的表面积为92cm2,则h的值为( )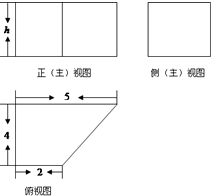

| A、4 | B、5 | C、6 | D、7 |
已知函数y=f(x)为定义在R上的奇函数,且x>0时,f(x)=lg(x2-ax+10),若函数y=f(x)的值域为R,则实数a的取值范围是( )
A、(-∞,-2
| ||||
B、(-2
| ||||
C、(-2
| ||||
D、[6,2
|
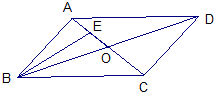 如图,在平面四边形ABCD中,AC,BD相交于点O,E为线段AO的中点,若
如图,在平面四边形ABCD中,AC,BD相交于点O,E为线段AO的中点,若