题目内容
已知tanα=m，m＞0，求：
（1）sinα、cosα的值；
（2）sin2α+2sinαcosα+3cos2α的值．
（1）sinα、cosα的值；
（2）sin2α+2sinαcosα+3cos2α的值．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）根据题意可得α在第一或第三象限，根据tanα=
=m、sin2α+cos2α=1，分类讨论求得sinα、cosα的值．
（2）根据sin2α+2sinαcosα+3cos2α=
=
，把已知代入计算求得结果．
| sinα |
| cosα |
（2）根据sin2α+2sinαcosα+3cos2α=
| sin2α+2sinαcosα+3cos2α |
| sin2α+cos2α |
| tan2α+2tanα+3 |
| tan2α+1 |
解答：
解：（1）∵tanα=m，m＞0，
∴α在第一或第三象限．
当α在第一象限时，根据tanα=
=m、sin2α+cos2α=1，
可得sinα=
，cosα=
．
当当α在第三象限时，根据tanα=
=m、sin2α+cos2α=1，
可得sinα=-
，cosα=-
．
（2）sin2α+2sinαcosα+3cos2α=
=
=
∴α在第一或第三象限．
当α在第一象限时，根据tanα=
| sinα |
| cosα |
可得sinα=
|
|
当当α在第三象限时，根据tanα=
| sinα |
| cosα |
可得sinα=-
|
|
（2）sin2α+2sinαcosα+3cos2α=
| sin2α+2sinαcosα+3cos2α |
| sin2α+cos2α |
| tan2α+2tanα+3 |
| tan2α+1 |
| m2+2m+3 |
| m2+1 |
点评：本题主要考查同角三角函数的基本关系的应用，以及三角函数在各个象限中的符号，属于中档题．
练习册系列答案
快捷英语周周练系列答案
相关题目
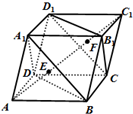已知平行六面体ABCD-A1B1C1D1，AC1与平面A1BD，CB1D1交于E，F两点．给出以下命题，其中真命题有若i是虚数单位，则复数
的实部与虚部之积为（ ）
| 2-i |
| 1+i |
A、
| ||
B、-
| ||
C、
| ||
D、-
|