题目内容
3.已知函数f(x)=x2+lnx(1)求y=-f(x)的单调区间;
(2)若函数g(x)=ax-f(x)存在极值,且所有极值之和大于5-ln$\frac{1}{2}$,求a的取值范围.
分析 (1)求出函数的导数,根据导函数的符号,求出函数的单调区间即可;
(2)方程2x2-ax+1=0在(0,+∞)上有根,根据二次函数的性质得到关于a的不等式组,解出即可.
解答 解:(1)y′=-2x-$\frac{1}{x}$=-$\frac{{2x}^{2}+1}{x}$<0,
故函数y=-f(x)在(0,+∞)递减;
(2)g(x)=ax-x2-lnx,(x>0),
g′(x)=a-2x-$\frac{1}{x}$=$\frac{-{2x}^{2}+ax-1}{x}$,(x>0),
∵g(x)存在极值,
∴g′(x)=0在(0,+∞)上有根,
即方程2x2-ax+1=0在(0,+∞)上有根.
设方程2x2-ax+1=0的两根为x1,x2,
由韦达定理得:$\left\{\begin{array}{l}{{x}_{1}{•x}_{2}=\frac{1}{2}>0}\\{{x}_{1}{+x}_{2}=\frac{a}{2}>0}\end{array}\right.$,
所以方程的根必为两不等正根.
f(x1)+f(x2)=a(x1+x2)-(x12+x22)-(lnx1+lnx2)
=$\frac{{a}^{2}}{2}$-$\frac{{a}^{2}}{4}$+1-ln$\frac{1}{2}$>5-ln$\frac{1}{2}$,
∴a2>16,
又a2>16满足方程2x2-ax+1=0判别式大于零,
故所求取值范围为(4,+∞).
点评 本题考查了函数的单调性问题,考查导数的应用以及二次函数的性质,是一道中档题.

练习册系列答案
相关题目
 ,下列命题正确的是( )
,下列命题正确的是( ) , 则
, 则
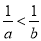
 ,则
,则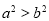
 ,则
,则 如图是正方体平面展开图,在这个正方体中:
如图是正方体平面展开图,在这个正方体中: