题目内容
已知椭圆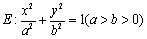 过点
过点 ,离心率为
,离心率为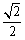 .
.
(1)若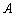 是椭圆
是椭圆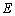 的上顶点,
的上顶点,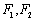 分别是左右焦点,直线
分别是左右焦点,直线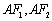 分别交椭圆于
分别交椭圆于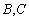 ,直线
,直线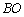 交
交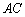 于D,求证
于D,求证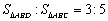 ;
;
(2)若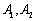 分别是椭圆
分别是椭圆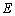 的左右顶点,动点
的左右顶点,动点 满足
满足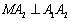 ,且
,且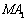 交椭圆
交椭圆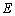 于点
于点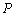 .
.
求证: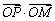 为定值.
为定值.
 (1)易得
(1)易得 且
且 ,
,
解得
所以,椭圆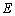 的方程为
的方程为 ;
;
所以, ,
,
所以,直线 ,直线
,直线
将  代入椭圆方程可得
代入椭圆方程可得 ,
,
所以 ,同理可得
,同理可得 ,
,
所以直线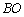 为
为 ,
,
联立 ,得交点
,得交点 ,
,
 所以,
所以, ,即
,即
所以, ;
;
(2)设 ,
, ,
,
易得直线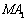 的方程为
的方程为 ,
,
代入椭圆 ,得
,得 ,
,
由 得,
得, ,
,
从而 ,
,
所以 .
.

练习册系列答案
相关题目
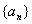 前项和
前项和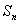 且
且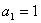 ,
,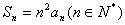
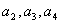
 的表达式,并用数学归纳法证明猜想.
的表达式,并用数学归纳法证明猜想.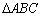 中,
中,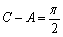 ,
,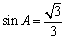 .
.  的值;
的值;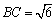 ,求
,求 且
且 的部分图像如图所示,则
的部分图像如图所示,则 的值为 .
的值为 .
 ,
, ,
,
 ,则四边形ABCD的面积是 .
,则四边形ABCD的面积是 . 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度.已知曲线 (
( 为参数)和曲线
为参数)和曲线 相交于
相交于 两点,求
两点,求 中点的直角坐标.
中点的直角坐标.

 中,已知
中,已知 ,点E是BC的中点,点F在CD上,若
,点E是BC的中点,点F在CD上,若 则
则 的值是 .
的值是 .