题目内容
14.若(x-$\frac{1}{x}$)n的二项展开式中所有项的二项式系数和为64,则常数项为-20(用数字作答)分析 由条件利用二项式系数的性质求得n=6,在二项展开式的通项公式中,令x的幂指数等于0,求出r的值,即可求得常数项.
解答 解:由题意可得2n=64,n=6,∴(x-$\frac{1}{x}$)n=(x-$\frac{1}{x}$)6,
它的展开式的通项公式为Tr+1=${C}_{6}^{r}$•(-1)r•x6-2r,令6-2r=0,求得r=3,
可得常数项为-${C}_{6}^{3}$=-20,
故答案为:-20.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
9.已知全集U=R,P=(0,1],Q={x|2x≤1},则P∪Q=( )
| A. | (-∞,1) | B. | (1,+∞) | C. | (-∞,1] | D. | [1,+∞) |
6.已知l,m,n是不同的直线,α,β,γ是不重合的平面,下列命题中正确的个数为( )
①若m⊥α,m⊥β,则α∥β;②若α⊥γ,β⊥γ,则α∥β
③若m∥α,m∥β,则α∥β;④l∥α,m?α,则l∥m.
①若m⊥α,m⊥β,则α∥β;②若α⊥γ,β⊥γ,则α∥β
③若m∥α,m∥β,则α∥β;④l∥α,m?α,则l∥m.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.已知集合A={0,a-2,3},若{-2,0}⊆A,则实数a的值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
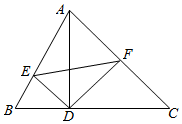 在△ABC中,AB=4,AC=6,∠BAC=60°.点A在边BC上的投影为点D.
在△ABC中,AB=4,AC=6,∠BAC=60°.点A在边BC上的投影为点D. 如图,在边长分别为f(x)与g(x)和2π的矩形内有由函数y=sinx的图象和x轴围成的区域(阴影部分),李明同学用随机模拟的方法估算该区域的面积.若在矩形内每次随机产生9000个点,并记录落在该区域内的点的个数.经过多次试验,计算出落在该区域内点的个数平均值为3000个,若π的近似值为3,则该区域的面积约为( )
如图,在边长分别为f(x)与g(x)和2π的矩形内有由函数y=sinx的图象和x轴围成的区域(阴影部分),李明同学用随机模拟的方法估算该区域的面积.若在矩形内每次随机产生9000个点,并记录落在该区域内的点的个数.经过多次试验,计算出落在该区域内点的个数平均值为3000个,若π的近似值为3,则该区域的面积约为( )