题目内容
2.从3名男同学,2名女同学中任选2人参加体能测试,则选到的2名同学至少有一名女同学的概率是$\frac{7}{10}$.分析 先求出基本事件总数,由选到的2名同学至少有一名女同学的对立事件为选到的2名同学都是男同学,利用对立事件概率计算公式能求出选到的2名同学至少有一名女同学的概率.
解答 解:从3名男同学,2名女同学中任意2人参加体能测试,
基本事件总数n=${C}_{5}^{2}=10$,
选到的2名同学至少有一名女同学的对立事件为选到的2名同学都是男同学,
∴选到的2名同学至少有一名女同学的概率:
p=1-$\frac{{C}_{3}^{2}}{{C}_{5}^{2}}$=$\frac{7}{10}$.
故答案为:$\frac{7}{10}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
12.执行如图的程序,若输出的值为2,则输入的值构成的集合是( )


| A. | {2} | B. | {1,2,-1,-2} | C. | {1,-1} | D. | {2,-2} |
13.阅读算法框图,如果输出的函数值在区间[1,8]上,则输入的实数x的取值范围是( )
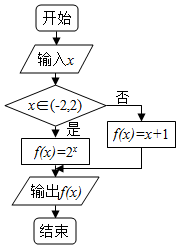

| A. | [0,2) | B. | [2,7] | C. | [2,4] | D. | [0,7] |
17.执行如图所示的程序框图,则输出的s=( )
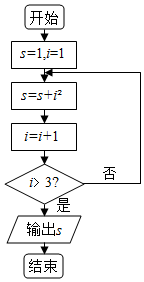

| A. | 6 | B. | 15 | C. | 25 | D. | 3 |
11.设命题p:?x∈N,x3<3x,则?p为( )
| A. | ?x∈N,x3<3x | B. | ?x∈N,x3≥3x | C. | ?x∈N,x3≥3x | D. | ?x∈N,x3=3x |
12.已知函数f(x)=2sin(2x+φ)(|φ|<$\frac{π}{2}}$)图象过点(0,$\sqrt{3}}$),则f(x)图象的一个对称中心是( )
| A. | $(-\frac{π}{3},0)$ | B. | $(-\frac{π}{6},0)$ | C. | $(\frac{π}{6},0)$ | D. | $(\frac{π}{12},0)$ |