题目内容
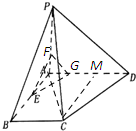
 已知四棱锥P-ABCD中,底面ABCD为直角梯形,BC∥AD,∠BAD=90°,且PA=AB=BC=1,AD=2,PA⊥平面ABCD,E为AB的中点.
已知四棱锥P-ABCD中,底面ABCD为直角梯形,BC∥AD,∠BAD=90°,且PA=AB=BC=1,AD=2,PA⊥平面ABCD,E为AB的中点.(I)证明:PC⊥CD;
(II)在线段PA上是否存在一点F,使EF∥平面PCD,若存在,求
| AF |
| FP |
考点:直线与平面平行的判定,空间中直线与直线之间的位置关系,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)首先根据已知条件,利用线面垂直的判定定理,证出线面垂直,进一步转化成线线垂直.
(Ⅱ)首先假设存在一点P,使得EF∥平面PCD,进一步利用面面平行转化成线面平行,最后得出结论成立,说明点的存在.
(Ⅱ)首先假设存在一点P,使得EF∥平面PCD,进一步利用面面平行转化成线面平行,最后得出结论成立,说明点的存在.
解答:
(Ⅰ)证明:平面ABCD,CD?平面ABCD.
∴PA⊥CD.
因为ABCD为直角梯形,且AB=BC=1,
∴AC=
,取AD的中点M,连接CM、CA,
易知四边形ABCM为矩形,
所以AC=CD=
=
,
因为AD=2,所以△ACD为直角三角形,
∴AC⊥CD,
又PA∩AC=A.
所以CD⊥平面PAC,
PC?平面PAC.
∴PC⊥CD.
(Ⅱ)解:假设在PA上存在一点F,当
=
时,EF∥平面PCD.
取AM的中点G,则GE为△ABM的中位线,
所以EG∥BM,
又因为四边形ABCM为矩形,
所以BM∥CD,
∴EG∥CD.
因为
=
,在PA上取一点F,使
=
,
则GF∥PD.
∵EG∩GF=G,
所以平面EGF∥平面PCD.
因为EF?平面EGF.所以EF∥平面PCD.
即当
=
时,EF∥平面PCD.
∴PA⊥CD.
因为ABCD为直角梯形,且AB=BC=1,
∴AC=
| 2 |
易知四边形ABCM为矩形,
所以AC=CD=
| CM2+AM2 |
| 2 |
因为AD=2,所以△ACD为直角三角形,
∴AC⊥CD,
又PA∩AC=A.
所以CD⊥平面PAC,
PC?平面PAC.
∴PC⊥CD.
(Ⅱ)解:假设在PA上存在一点F,当
| AF |
| FP |
| 1 |
| 3 |
取AM的中点G,则GE为△ABM的中位线,
所以EG∥BM,
又因为四边形ABCM为矩形,
所以BM∥CD,
∴EG∥CD.
因为
| AG |
| GD |
| 1 |
| 3 |
| AF |
| FP |
| 1 |
| 3 |
则GF∥PD.
∵EG∩GF=G,
所以平面EGF∥平面PCD.
因为EF?平面EGF.所以EF∥平面PCD.
即当
| AF |
| FP |
| 1 |
| 3 |

点评:本题考查的知识要点:线面垂直的判定定理,线面垂直与线线垂直之间的转化,存在性问题的应用,面面平行与线面平行之间的转化.属于中等题型.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
已知空间两个点A,B的坐标分别为A(1,2,2),B(2,-2,1),则|AB|=( )
| A、18 | ||
| B、12 | ||
C、3
| ||
D、2
|
在区间[-2,1]上随机取一个数,则该数是正数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
