题目内容
设不等式log3x<0的解集为M.
(1)求集合M;
(2)若a,b∈M,试比较ab+1与a+b的大小.
(1)求集合M;
(2)若a,b∈M,试比较ab+1与a+b的大小.
考点:指、对数不等式的解法,不等式比较大小
专题:不等式的解法及应用
分析:(1)直接利用对数的运算法则以及对数不等式的解法,即可求集合M;
(2)通过作差法直接比较ab+1与a+b的大小.
(2)通过作差法直接比较ab+1与a+b的大小.
解答:
解:(1)log3x<0=log31,∴0<x<1,∴M={x|0<x<1}
(2)由(1)和a,b∈M可知0<a<1,0<b<1,
∴(ab+1)-(a+b)=(a-1)(b-1)>0,∴ab+1>a+b.
(2)由(1)和a,b∈M可知0<a<1,0<b<1,
∴(ab+1)-(a+b)=(a-1)(b-1)>0,∴ab+1>a+b.
点评:本题考查对数不等式的解法,数值大小的比较,考查基本知识的应用.

练习册系列答案
相关题目
已知f(x)=x2+cosα,则曲线f(x)在x=
处的切线斜率为( )
| π |
| 6 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
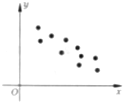 设(x1,y1),(x2,y2),…(xn,yn)是变量x,和y的n个样本点,直线l是由这样样本点通过最小二乘法得到的线性回归方程(如图),则下列结论中正确的是( )
设(x1,y1),(x2,y2),…(xn,yn)是变量x,和y的n个样本点,直线l是由这样样本点通过最小二乘法得到的线性回归方程(如图),则下列结论中正确的是( )| A、x和y正相关 |
| B、x和y的相关系数为直线l的斜率 |
| C、当n为偶数时,分布在l两侧的样本点的个数一定相同 |
| D、x和y的相关系数在-1到0之间 |
给定两个命题:
p:?a∈R,使y=x2+
为偶函数;
q:?x∈R,(sinx-1)(cosx-1)≥0恒成立.
其中正确的命题的为( )
p:?a∈R,使y=x2+
| a |
| x+1 |
q:?x∈R,(sinx-1)(cosx-1)≥0恒成立.
其中正确的命题的为( )
| A、p∧q | B、p∧¬q |
| C、p∨¬q | D、¬p∨q |
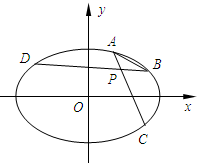 如图所示,在平面直角坐标系xOy中,设椭圆E:
如图所示,在平面直角坐标系xOy中,设椭圆E: