题目内容
6.在平面直角坐标系xOy中,直线1与曲线y=x2(x>0)和y=x3(x>0)均相切,切点分别为A(x1,y1)和B(x2,y2),则$\frac{{x}_{1}}{{x}_{2}}$的值为$\frac{4}{3}$.分析 求出导数得出切线方程,即可得出结论.
解答 解:由y=x2,得y′=2x,切线方程为y-x12=2x1(x-x1),即y=2x1x-x12,
由y=x3,得y′=3x2,切线方程为y-x23=3x22(x-x2),即y=3x22x-2x23,
∴2x1=3x22,x12=2x23,
两式相除,可得$\frac{{x}_{1}}{{x}_{2}}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 考查学生会利用导数求曲线上某点的切线方程的斜率,本题的突破点是分别求出切线方程得到x1,x2的关系.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
16.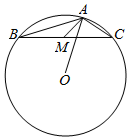 已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
 已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
14.一圆锥的侧面积是其底面积的2倍,若圆锥的高为$\sqrt{3}$,则其表面积为( )
| A. | $\frac{3\sqrt{3}π}{2}$ | B. | 6π | C. | 3π | D. | 3$\sqrt{3}$π |
18.设全集U={0,1,2,3,4},∁UA={1,2},B={1,3},则A∪B等于( )
| A. | {2} | B. | {1,2,3} | C. | {0,1,3,4} | D. | {0,1,2,3,4} |
16.“lgx,lgy,lgz成等差数列”是“y2=xz”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |