题目内容
20.已知函数f(x)=$\left\{\begin{array}{l}{\frac{x}{3},x∈[0,\frac{1}{2}]}\\{\frac{{2x}^{3}}{x+1},x∈(\frac{1}{2},1]}\end{array}\right.$,函数g(x)=ax-$\frac{a}{2}$+3(a>0),若对任意x1∈[0,1],总存在x2$∈[0,\frac{1}{2}]$,使得f(x1)=g(x2)成立,则实数a的取值范围是( )| A. | (-∞,4] | B. | (-∞,6] | C. | [-4,+∞) | D. | [6,+∞) |
分析 根据一次函数,以及导数研究函数f(x)的单调性,求出函数f(x)与g(x)的值域,根据恒成立关系转化为两个函数的值域问题,进行求解即可.
解答 解:当$\frac{1}{2}$<x≤1时,f(x)=$\frac{2{x}^{3}}{x+1}$,则f′(x)=$\frac{2{x}^{2}(2x+3)}{(x+1)^{2}}$>0,此时函数为增函数,
则f($\frac{1}{2}$)<f(x)≤f(1),
即$\frac{1}{6}$<f(x)≤1,
当0≤x≤$\frac{1}{2}$时,f(x)=$\frac{x}{3}$为增函数,
则0≤f(x)≤$\frac{1}{6}$,
综上所述,当x∈[0,1]时,0≤f(x)≤1,
当x2$∈[0,\frac{1}{2}]$,g(0)≤g(x)≤g($\frac{1}{2}$),
即3-$\frac{a}{2}$≤g(x)≤3,
若对任意x1∈[0,1],总存在x2$∈[0,\frac{1}{2}]$,使得f(x1)=g(x2)成立,
则[0,1]⊆[3-$\frac{a}{2}$,3],则3-$\frac{a}{2}$≤0,即$\frac{a}{2}$≥3,
则a≥6,
故实数a的取值范围是[6,+∞),
故选:D.
点评 本题主要考查函数恒成立问题,根据导数研究函数的单调性,求出函数的值域,根据条件建立值域之间的关系是解决本题的关键.综合考查学生是运算和推理能力.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
10. 第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
(Ⅰ)根据表格中两组数据完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);
(Ⅱ)甲、乙、丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多(假设两国代表团获得的金牌数不会相等),规定甲、乙、丙必须在两个代表团中选一个,已知甲、乙猜中国代表团的概率都为$\frac{4}{5}$,丙猜中国代表团的概率为$\frac{3}{5}$,三人各自猜哪个代表团的结果互不影响.现让甲、乙、丙各猜一次,设三人中猜中国代表团的人数为X,求X的分布列及数学期望EX.
 第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第31届夏季奥林匹克运动会将于2016年8月5日-21日在巴西里约热内卢举行.下表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).| 第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
| 中国 | 38 | 51 | 32 | 28 | 16 |
| 俄罗斯 | 24 | 23 | 27 | 32 | 26 |
(Ⅱ)甲、乙、丙三人竞猜今年中国代表团和俄罗斯代表团中的哪一个获得的金牌数多(假设两国代表团获得的金牌数不会相等),规定甲、乙、丙必须在两个代表团中选一个,已知甲、乙猜中国代表团的概率都为$\frac{4}{5}$,丙猜中国代表团的概率为$\frac{3}{5}$,三人各自猜哪个代表团的结果互不影响.现让甲、乙、丙各猜一次,设三人中猜中国代表团的人数为X,求X的分布列及数学期望EX.
15.2015年9月12日青岛2015世界休闲体育大会隆重开幕.为普及体育知识,某校学生社团组织了14人进行“体育知识竞赛”活动,每人回答3个问题,答对题目个数及对应人数统计结果见表:
根据表格信息解答以下问题:
(Ⅰ)从14人中任选3人,求3人答对题目个数之和为6的概率;
(Ⅱ)从14人中任选2人,用X表示这2人答对题目个数之和,求随机变量X的分布列和数学期望EX.
| 答对题目个数 | 0 | 1 | 2 | 3 |
| 人数 | 3 | 2 | 5 | 4 |
(Ⅰ)从14人中任选3人,求3人答对题目个数之和为6的概率;
(Ⅱ)从14人中任选2人,用X表示这2人答对题目个数之和,求随机变量X的分布列和数学期望EX.
12.在一次对人体脂肪百分比和年龄关系的研究中,研究人员获得如下一组样本数据:
由表中数据求得y关于x的线性回归方程$\stackrel{∧}{y}$=0.6x+$\stackrel{∧}{a}$,若年龄x的值为50,则脂肪y的估计值为32.
| 年龄x | 21 | 24 | 34 | 41 |
| 脂肪y | 9.5 | 17.5 | 24.9 | 28.1 |
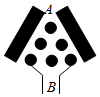 将一个半径适当的小球从如图所示的A入口处,向下自由下落.小球在下落的过程中,将3次遇到黑色障碍物,每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,最后通过黑色区域.
将一个半径适当的小球从如图所示的A入口处,向下自由下落.小球在下落的过程中,将3次遇到黑色障碍物,每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$,最后通过黑色区域.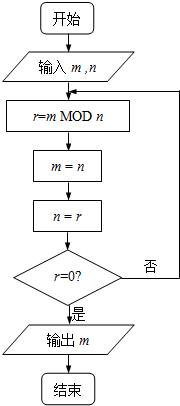 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“m MOD n”表示m除以n的余数),若输入的m,n分别为495,135,则输出的m=( )