题目内容
12．在一次对人体脂肪百分比和年龄关系的研究中，研究人员获得如下一组样本数据：| 年龄x | 21 | 24 | 34 | 41 |
| 脂肪y | 9.5 | 17.5 | 24.9 | 28.1 |
分析 求出数据中心（$\overline{x}，\overline{y}$），代入回归方程得出$\stackrel{∧}{a}$，再将x=50代入回归方程得出答案．
解答 解：$\overline{x}$=$\frac{21+24+34+41}{4}$=30，$\overline{y}$=$\frac{9.5+17.5+24.9+28.1}{4}$=20．
代入回归方程得20=0.6×30+$\stackrel{∧}{a}$，解得$\stackrel{∧}{a}$=2．
∴回归方程为$\stackrel{∧}{y}$=0.6x+2．
当x=50时，$\stackrel{∧}{y}$=0.6×50+2=32．
故答案为：32．
点评 本题考查了线性回归方程的特点及利用回归方程进行数值估计，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
2．若$\overrightarrow{a}$=（1，2），$\overrightarrow b=（{m，1}）$，若$\overrightarrow a$∥$\overrightarrow b$，则m=（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | 2 | D． | -2 |
3．若全集U=R，集合A={x|x2-x-2≥0}，B={x|log3（2-x）≤1}，则A∩（∁UB）=（ ）
| A． | {x|x＜2} | B． | {x|x＜-1或x≥2} | C． | {x|x≥2} | D． | {x|x≤-1或x＞2} |
20．已知函数f（x）=$\left\{\begin{array}{l}{\frac{x}{3}，x∈[0，\frac{1}{2}]}\\{\frac{{2x}^{3}}{x+1}，x∈（\frac{1}{2}，1]}\end{array}\right.$，函数g（x）=ax-$\frac{a}{2}$+3（a＞0），若对任意x1∈[0，1]，总存在x2$∈[0，\frac{1}{2}]$，使得f（x1）=g（x2）成立，则实数a的取值范围是（ ）
| A． | （-∞，4] | B． | （-∞，6] | C． | [-4，+∞） | D． | [6，+∞） |
7．
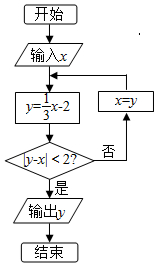执行如图所示的程序框图，若输入x=9，则输出的y的值为（ ）
执行如图所示的程序框图，若输入x=9，则输出的y的值为（ ）| A． | -$\frac{23}{9}$ | B． | 1 | C． | $\frac{8}{9}$ | D． | -$\frac{5}{3}$ |
吉林市某中学利用周末组织教职员工进行了一次冬季户外健身活动，有N人参加，现将所有参加人员按年龄情况分为[20，25），[25，30），[30，35），[35，40），[40，45），[45，50），[50，55）等七组，其频率分布直方图如图所示．已知[35，40）之间的参加者有8人．
4．已知集合M={x|-1≤x＜3}，集合$N=\left\{{x\left|{y=\sqrt{-{x^2}-x+6}}\right.}\right\}$，则M∪N=（ ）
| A． | M | B． | N | C． | {x|-1≤x≤2} | D． | {x|-3≤x＜3} |