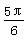题目内容
已知a＝(3，4)，b＝(4，3)，求x、y的值使(xa＋yb)⊥a，且|xa＋yb|＝1.
解：由a＝(3，4)，b＝(4，3)，有xa＋yb＝(3x＋4y，4x＋3y)．
(xa＋yb)⊥a(xa＋yb)·a＝03(3x＋4y)＋4(4x＋3y)＝0，即25x＋24y＝0.①
又|xa＋yb|＝1|xa＋yb|2＝1，
有(3x＋4y)2＋(4x＋3y)2＝1，
整理得25x2＋48xy＋25y2＝1，
即x(25x＋24y)＋24xy＋25y2＝1，②
由①②有24xy＋25y2＝1，③
将①变形代入③可得y＝±
，
再代回①得
练习册系列答案
相关题目
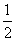的等比数列，且1－a2是a1与1＋a3的等比中项，前n项和为Sn；数列{bn}是等差数列，b1＝8，其前n项和Tn满足Tn＝nλ·bn＋1(λ为常数，且λ≠1)．
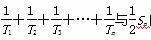的大小．
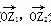分别对应复数z1，z2，且z1＝
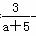＋(10－a2)i，z2＝
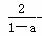＋(2a－5)i(a∈R)，若
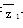＋z2是实数．
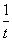b，m∈R，k、t为正实数．
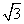cos x＋sin x(x∈R)的图象向左平移m(m＞0)个单位长度后，所得到的图象关于y轴对称，则m的最小值是( )
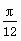B. 
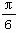
D. 