题目内容
11.已知f(x)=$\left\{\begin{array}{l}{{x}^{2}-4x+3,x≤0}\\{-{x}^{2}-2x+3,x>0}\end{array}\right.$,当x∈[-2,2]时不等式f(x+a)≥f(2a-x)恒成立,则实数a的最小值是4.分析 分析分段函数的单调性,得知函数单调递减,不等式可整理为2x≤a,只需求出左式的最大值即可.
解答 解:当x≤0时,f(x)=x2-4x+3,
对称轴为x=2,故在区间内递减,f(x)≥f(0)=3;
当x>0时,f(x)=-x2-2x+3,
对称轴为x=-2,故在区间内递减且f(x)<f(0)=3;
可知函数f(x)在整个区间内递减,
∴x∈[-2,2]时不等式f(x+a)≥f(2a-x)恒成立,
∴x+a≤2a-x,
∴2x≤a,
∴a≥4,
故答案为4.
点评 考查了分段函数的单调性和单调性的利用.

练习册系列答案
相关题目
3.点P是抛物线y2=4x上一动点,则点P到点A(0,-1)的距离与到直线x=-1的距离和的最小值是( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
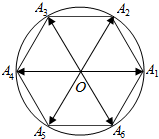 已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$.
已知正六边形A1A2…A6内接于圆O,点P为圆O上一点,向量$\overrightarrow{OP}$与$\overrightarrow{O{A_i}}$的夹角为θi(i=1,2,…,6),若将θ1,θ2,…,θ6从小到大重新排列后恰好组成等差数列,则该等差数列的第3项为$\frac{5π}{12}$. 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.