题目内容
14.已知函数f(x)=cos2x+2$\sqrt{3}$sinxcosx-sin2x,x∈R.(1)求f(x)的最小正周期和值域;
(2)△ABC中,角A,B,C所对的边分别是a,b,c,若f($\frac{A}{2}$)=2且asinA=bsinC,试判断△ABC的形状.
分析 (1)由三角函数公式化简可得f(x)=2sin(2x+$\frac{π}{6}$),易得周期和值域;
(2)由(1)和三角形的内角范围可得A=$\frac{π}{3}$,由正余弦定理可得b=c,可判三角形形状.
解答 解:(1)化简可得f(x)=cos2x+2$\sqrt{3}$sinxcosx-sin2x
=$\sqrt{3}$sin2x+cos2x=2sin(2x+$\frac{π}{6}$),
∴f(x)的最小正周期T=$\frac{2π}{2}$=π,函数的值域为[-2,2];
(2)∵f($\frac{A}{2}$)=2sin(A+$\frac{π}{6}$)=2,∴sin(A+$\frac{π}{6}$)=1.
∵0<A<π,∴A+$\frac{π}{6}$=$\frac{π}{2}$,∴A=$\frac{π}{3}$.
由asinA=bsinC和正弦定理可得a2=bc,
再由余弦定理可得a2=b2+c2-2bccosA,
∴(b-c)2=0,∴b=c,∴B=C=$\frac{π}{3}$.
∴△ABC为等边三角形.
点评 本题考查正余弦定理解三角形,涉及三角函数公式和三角函数的性质,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.若角α的终边过点(-1,2),则sin(π-2α)•cos(π-2α)的值为( )
| A. | -$\frac{12}{25}$ | B. | $\frac{12}{25}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
10.已知等比数列{an}的公比为q=-$\frac{1}{2}$.
(1)若a4=$\frac{1}{8}$,求数列{an}的前n项和;
(2)证明:对任意k∈N*,ak+2是ak与ak+1的等差中项.
(1)若a4=$\frac{1}{8}$,求数列{an}的前n项和;
(2)证明:对任意k∈N*,ak+2是ak与ak+1的等差中项.
9.如图,在平面四边形ABCD中,AB=1,$BC=\sqrt{3}+1$,$AD=\sqrt{6}$,∠ABC=120°,∠DAB=75°,则CD=( )
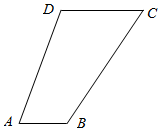

| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{2}+1$ |
4.下列四条直线,倾斜角最大的是( )
| A. | y=-x+1 | B. | y=x+1 | C. | y=2x+1 | D. | x=1 |
 (文科)四棱镜P-ABCD中,PD⊥平面ABCD,2AD=AB=BC=2a,AD∥BC,PD=$\sqrt{3}$a,∠DAB=60°,Q是PB的中点.
(文科)四棱镜P-ABCD中,PD⊥平面ABCD,2AD=AB=BC=2a,AD∥BC,PD=$\sqrt{3}$a,∠DAB=60°,Q是PB的中点. 在四棱锥P-ABCD中,平面四边形ABCD中AD∥BC,∠BAD为二面角B-PA-D一个平面角.
在四棱锥P-ABCD中,平面四边形ABCD中AD∥BC,∠BAD为二面角B-PA-D一个平面角.