题目内容
19.对于问题:“已知关于x的不等式ax2+bx+c>0的解集为(-1,2),解关于x的不等式ax2-bx+c>0”,给出如下一种解法:由ax2+bx+c>0的解集为(-1,2),得a(-x)2+b(-x)+c>0的解集为(-2,1),即关于x的不等式ax2-bx+c>0的解集为(-2,1).参考上述解法,若关于x的不等式$\frac{k}{x+a}$+$\frac{x+b}{x+c}$<0的解集为(-2,-$\frac{1}{3}$)∪($\frac{1}{2}$,1),则关于x的不等式$\frac{kx}{ax+1}$+$\frac{bx+1}{cx+1}$<0的解集为(-3,$-\frac{1}{2}$)∪(1,2).
分析 根据不等式的新解法,进行类比求解即可.
解答 解:由$\frac{k}{x+a}$+$\frac{x+b}{x+c}$<0的解集为(-2,-$\frac{1}{3}$)∪($\frac{1}{2}$,1),
得$\frac{k}{\frac{1}{x}+a}$+$\frac{\frac{1}{x}+b}{\frac{1}{x}+c}$<0,即$\frac{kx}{ax+1}$+$\frac{bx+1}{cx+1}$<0,
由-2<$\frac{1}{x}$<-$\frac{1}{3}$或$\frac{1}{2}$<$\frac{1}{x}$<1,
得-3<x<$-\frac{1}{2}$或1<x<2,
即不等式$\frac{kx}{ax+1}$+$\frac{bx+1}{cx+1}$<0的解集为(-3,$-\frac{1}{2}$)∪(1,2),
故答案为:(-3,$-\frac{1}{2}$)∪(1,2)
点评 本题主要考查不等式的求解,利用不等式的新解法,利用类比法是解决本题的关键.

练习册系列答案
相关题目
4.复数z满足z(1+$\sqrt{3}\\;i$i)=|1+$\sqrt{3}$i|,则z等于( )
| A. | 1-$\sqrt{3}$i | B. | 1 | C. | $\frac{1}{2}$-$\frac{\sqrt{3}}{2}$i | D. | $\frac{\sqrt{3}}{2}$-$\frac{1}{2}$i |
11.已知向量$\overrightarrow{m}$=(1,cosθ),$\overrightarrow{n}$=(sinθ,-2),且$\overrightarrow{m}$⊥$\overrightarrow{n}$,则sin2θ+6cos2θ的值为( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | -2 |
8.若tanα=$\frac{1}{3}$,则cos($\frac{π}{2}$+2α)=( )
| A. | -$\frac{4}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
9.若a>b,c>d,则下面不等式中成立的一个是( )
| A. | a+d>b+c | B. | ac>bd | C. | ac2>bc2 | D. | d-a<c-b |
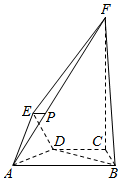 如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.
如图几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,CB=CD=2.面EAD⊥面ABCD,面FCB⊥面ABCD,且CF⊥BC.