题目内容
在正三棱锥P-ABC中，M，N分别是PB，PC的中点，若截面AMN⊥平面PBC，则此棱锥中侧面积与底面积的比为考点：棱柱、棱锥、棱台的体积
专题：综合题,空间位置关系与距离
分析：画出图形，说明棱锥的棱长等于底面三角形的高，设出高，然后求出侧面面积，底面面积即可得到比值．
解答：
解：取MN的中点H，连接PH交BC于E，连接AE、AH，因为正三棱锥P-ABC中，所以PA=PB=PC，M，N是侧棱PB、PC的中点，所以AH⊥MN，
截面AMN垂直于侧面PBC，所以BC⊥平面PAE，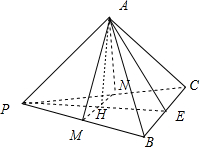
∴AH是PE的垂直平分线．所以，PA=AE
设PA=a，所以AB=
a，
棱锥的侧面积为：3×
×
a×
=
a2．
底面面积为：
（
a）2=
a2．
棱锥的侧面积与底面积的比：
：1．
故答案为：
：1．
截面AMN垂直于侧面PBC，所以BC⊥平面PAE，
∴AH是PE的垂直平分线．所以，PA=AE
设PA=a，所以AB=
2
| ||
| 3 |
棱锥的侧面积为：3×
| 1 |
| 2 |
2
| ||
| 3 |
a2-(
|
| 2 |
底面面积为：
| ||
| 4 |
2
| ||
| 3 |
| ||
| 3 |
棱锥的侧面积与底面积的比：
| 6 |
故答案为：
| 6 |
点评：本题考查空间几何体的想象能力，逻辑推理能力与计算能力，难度中等．
练习册系列答案
习题精选系列答案
相关题目
定义在R上的函数f（x）满足（x+2）•f′（x）＜0（其中f′（x）是函数f（x）的导数），又a=f（log23），b=f（1），c=f（ln3），则（ ）
| A、a＜c＜b |
| B、b＜c＜a |
| C、c＜a＜b |
| D、c＜b＜a |
已知a+2b=2（a，b＞0），则ab的最大值为（ ）
A、
| ||
| B、2 | ||
| C、3 | ||
D、
|