Question

3．已知双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右焦点为F，过点F向双曲线的一条渐进线引垂线，垂足为M，交另一条渐近线于N，若2$\overrightarrow{MF}$=$\overrightarrow{FN}$，则双曲线的离心率$\frac{2\sqrt{3}}{3}$．

Answer 1

分析 由题意可知F为MN的三等分点，用a，b，c表示出△OMN的边长，利用勾股定理得出a，b的关系从而得出离心率．

解答 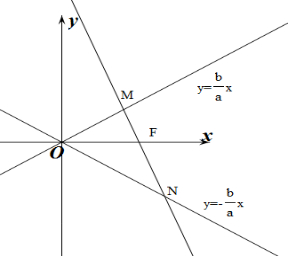解：双曲线的渐近线方程为y=±$\frac{b}{a}x$，设M在直线y=$\frac{b}{a}x$上，M（x₀，$\frac{b}{a}{x}_{0}$），F（c，0），
则MF=$\frac{bc}{\sqrt{{a}^{2}+{b}^{2}}}$=b，OM=$\sqrt{O{F}^{2}-M{F}^{2}}$=$\sqrt{{c}^{2}-{b}^{2}}$=a，
∵2$\overrightarrow{MF}$=$\overrightarrow{FN}$，∴FN=2b，
∴S_△OFN=2S_△OMF，
即$\frac{1}{2}×c×ON×sin∠NOF$=2×$\frac{1}{2}×ac×sin∠MOF$
∵∠MOF=∠NOF，
∴ON=2a，
在Rt△OMN中，由勾股定理得a²+9b²=4a²，
∴b²=$\frac{{a}^{2}}{3}$，
∴e=$\frac{\sqrt{{a}^{2}+{b}^{2}}}{a}$=$\frac{2\sqrt{3}}{3}$．
故答案为：$\frac{2\sqrt{3}}{3}$．

点评 本题考查了双曲线的简单性质，属于中档题．