题目内容
17.用1、2、3、4四个数字可以组成百位上不是3的无重复数字的三位数的个数是18.分析 先从1,2,4种选一个确定百位,其它位置的数的任意排,问题得以解决.
解答 解:先从1,2,4种选一个确定百位,其它位置的数的任意排,故有A31A32=18种,
故答案为:18.
点评 本题考查分步计数原理,关键是分步,属于基础题.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
7.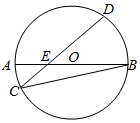 如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )
如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )
 如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )
如图,圆O的直径AB与弦CD交于点E,且E为OA的中点,若OA=2,∠BCD=30°,则线段CE的长为( )| A. | 1 | B. | $\frac{3\sqrt{5}}{5}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{3\sqrt{7}}{7}$ |
8.函数f(x)是定义在(0,+∞)上的单调函数,且对定义域内的任意x,均有f(f(x)-lnx-x3)=2,则f(e)=( )
| A. | e3+1 | B. | e3+2 | C. | e3+e+1 | D. | e3+e+2 |
12.运行如图的程序框图,若输出的y值随着输入的x的增大而增大,则a的取值不可能是( )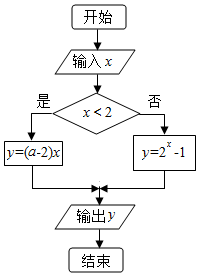

| A. | $\frac{5}{2}$ | B. | $\frac{7}{2}$ | C. | 3 | D. | 4 |
9.已知点M是△ABC所在平面内的一点,且满足5$\overrightarrow{AM}$=$\overrightarrow{AB}$+2$\overrightarrow{AC}$,则△AMB与△ABC的面积比为( )
| A. | $\frac{5}{2}$ | B. | $\frac{2}{5}$ | C. | $\frac{7}{5}$ | D. | $\frac{5}{7}$ |
7.已知函数f(x)=(x-a-1)(2x-a),g(x)=ln(x-a),若当x>a时,f(x)•g(x)≥0恒成立,则实数a的取值范围是( )
| A. | [0,+∞) | B. | [-2,0] | C. | (-∞,2] | D. | [-2,+∞) |
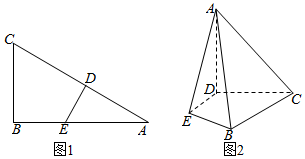 已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).
已知直角三角形ABC中,AC=6,BC=3,∠ABC=90°,点D,E分别是边AC,AB上的动点(不含A点),且满足$\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$(图1).将△ADE沿DE折起,使得平面ADE⊥平面BCDE,连结AB、AC(图2).