题目内容
8．奇函数f（x）在（-∞，0）上单调递减，且f（2）=0，则不等式f（x）＞0的解集是（ ）| A． | （-∞，-2）∪（0，2） | B． | （-∞，0）∪（2，+∞） | C． | （-2，0）∪（0，2） | D． | （-2，0）∪（2，+∞） |
分析 根据奇函数的性质求出f（-2）=0，由条件画出函数图象示意图，结合图象即可求出不等式的解集．
解答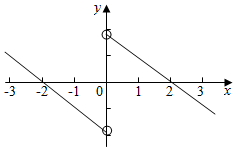 
解：∵f（x）为奇函数，且f（2）=0，在（-∞，0）是减函数，
∴f（-2）=-f（2）=0，f（x）在（0，+∞）内是减函数，
函数图象示意图，
∴不等式f（x）＞0的解集为（-∞，-2）∪（0，2），
故选A．
点评 本题考查函数的奇偶性、单调性的综合应用，正确画出函数的示意图是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
13．设命题p：?x∈R，x2+1＞0，则￢p为（ ）
| A． | $?{x_0}∈R，{x^2}+1＞0$ | B． | $?{x_0}∈R，{x^2}+1≤0$ | C． | $?{x_0}∈R，{x^2}+1＜0$ | D． | $?{x_0}∈R，{x^2}+1≤0$ |
19．函数f（x）=log3x+x-3的零点所在的区间是（ ）
| A． | （0，2） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
15．已知x，y∈（0，+∞），且满足$\frac{1}{x}+\frac{1}{2y}=2$，那么x+4y的最小值为（ ）
| A． | $\frac{3}{2}-\sqrt{2}$ | B． | $3+\frac{{\sqrt{2}}}{2}$ | C． | $\frac{3}{2}+\sqrt{2}$ | D． | $3-\frac{{\sqrt{2}}}{2}$ |