题目内容
已知l1过点P1(4,2),l2过点P2(-1,3),若l1∥l2,且l1与l2间距离最大,则l1的方程是 .
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:本题通过条件“l1与l2间距离最大”,分析得到直线l1、l2都直线P1P2垂直,从而得到直线的斜率,由点斜式写出直线的方程,得到本题结论.
解答:
解:∵l1过点P1(4,2),
∴过点P1(4,2)作直线l2的垂线,垂足为H,
则有P1H长为两直线l1、l2间的距离.
∵l2过点P2(-1,3),
∴P1H≤P1P2.
∴l1与l2间距离最大时,直线l1、l2都直线P1P2垂直.
∵k P1P2=
=-
.
∴直线l1、l2都的斜率均为5.
∴l1的方程是:y-2=5(x-4),即5x-y-18=0.
∴故答案为:5x-y-18=0.
∴过点P1(4,2)作直线l2的垂线,垂足为H,
则有P1H长为两直线l1、l2间的距离.
∵l2过点P2(-1,3),
∴P1H≤P1P2.
∴l1与l2间距离最大时,直线l1、l2都直线P1P2垂直.
∵k P1P2=
| 3-2 |
| -1-4 |
| 1 |
| 5 |
∴直线l1、l2都的斜率均为5.
∴l1的方程是:y-2=5(x-4),即5x-y-18=0.
∴故答案为:5x-y-18=0.
点评:本题考查了直线的点斜式方程,本题难度不大,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
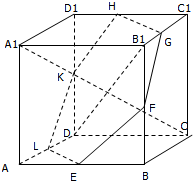 如图所示,正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求证:A1C⊥平面EFGHKL.
如图所示,正方体ABCD-A1B1C1D1中,E、F、G、H、K、L分别为AB、BB1、B1C1、C1D1、D1D、DA的中点,求证:A1C⊥平面EFGHKL.